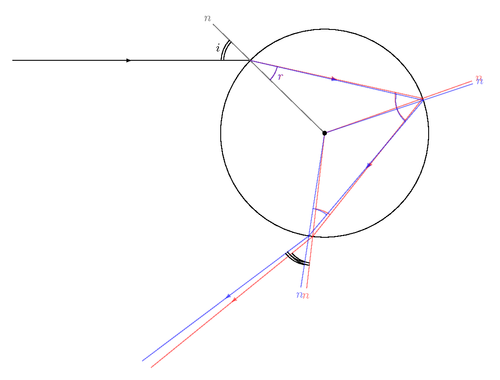
Rainbows form because light of different colors refracts differently in a drop of water. To understand a rainbow in detail, you need to consider all possible rays entering the drop, many raindrops at once, and the reflectivity for various angles at the back of the drop. The current figure shows only one ray entering the raindrop and visualizes the path of the red and blue rays. The index of refraction of the red ray is slightly exaggerated (less than one percent) for clarity. Observe that the angle of incidence is identical to the angle with which the rays finally exit the drop. Furthermore, the red internal angles are all identical, similar for the blue angles.
This figure was drawn for high school students because a physics textbook figure contained several errors and ultimately claimed the red and blue light exiting the raindrop as parallel rays.
Edit and compile if you like:
% Rainbows - Sun ray entering a rain drop
% Author: David Fokkema
\documentclass{article}
\usepackage{tikz}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{10pt}%
\usetikzlibrary{calc,decorations.markings}
% Draw an arc denoting an angle using start and delta angles
\newcommand{\drawarcdelta}[4]{
\draw ($#1+(#2:#4)$) arc[start angle=#2, delta angle=#3, radius=#4];
}
% Draw an arc with label denoting an angle using start and delta angles
\newcommand{\drawlabeledarcdelta}[6]{
\drawarcdelta{#1}{#2}{#3}{#4}
\node at ($#1+(#2+#3/2:#6)$) {#5};
}
\begin{document}
\begin{tikzpicture}[xscale=-1,
ray/.style={decoration={markings,mark=at position .5 with {
\arrow[>=latex]{>}}},postaction=decorate}
]
% Radius of raindrop
\pgfmathsetlengthmacro{\r}{3cm}
% Position where the incoming ray enters the raindrop, as a fraction of
% the height of the drop. If 0., the ray will enter in the middle of the
% drop, if 1., the ray will enter at the top of the drop.
\pgfmathsetmacro{\f}{.7}
% Various radii for drawing angle arcs and labels
\pgfmathsetlengthmacro{\arcradius}{.8cm}
\pgfmathsetlengthmacro{\dotradius}{.6cm}
\pgfmathsetlengthmacro{\arclabelradius}{1cm}
% Calculation of the angle of incidence
\pgfmathsetmacro{\incidentangle}{asin(\f)}
% Coordinates of origin and point of entry
\coordinate (O) at (0, 0);
\coordinate (A) at (\incidentangle:\r);
% Draw the drop and the incoming ray, as well as the angle of incidence
\draw (O) circle (\r);
\draw[ray] (A -| \r*3, 0) -- (A);
\draw[gray] (O) -- ($(O)!1.5!(A)$) node[pos=1.05] {$n$};
\drawarcdelta{(A)}{0}{\incidentangle}{\arcradius-1pt}
\drawlabeledarcdelta{(A)}{0}{\incidentangle}{\arcradius+1pt}
{$i$}{\arclabelradius}
% For each red and blue ray. The index of refraction for red light is
% slightly exaggerated, it should be 1.33.
\foreach \index/\color in {1.32/red, 1.34/blue} {
% Calculate angle of refraction
\pgfmathsetmacro{\refractedangle}{asin(sin(\incidentangle) / \index)}
% Calculate top angle (at O) in the triangle formed by O, the point of
% entry, and the point of internal reflection
\pgfmathsetmacro{\angleindrop}{180 - 2*\refractedangle}
% Coordinate of point of reflection
\coordinate (A') at (\incidentangle+\angleindrop:\r);
% Coordinate of point of exit
\coordinate (A'') at (\incidentangle+2*\angleindrop:\r);
\begin{scope}[opacity=.5, color=\color]
% Draw the light rays
\draw[ray] (A) -- (A');
\draw[ray] (A') -- (A'');
\draw[ray] (A'') -- ($(A'')+(2*\incidentangle+2*\angleindrop:2*\r)$);
% Draw the normal lines
\draw (O) -- ($(O)!1.5!(A')$) node[pos=1.05] {$n$};
\draw (O) -- ($(O)!1.5!(A'')$) node[pos=1.05] {$n$};
% Draw the arcs and labels
\drawlabeledarcdelta{(A)}{\incidentangle+180}{-\refractedangle}
{\arcradius}{$r$}{\arclabelradius}
\drawarcdelta{(A')}{\incidentangle+\angleindrop+180}{\refractedangle}
{\arcradius}
\drawarcdelta{(A')}{\incidentangle+\angleindrop+180}{-\refractedangle}
{\arcradius}
\drawarcdelta{(A'')}{\incidentangle+2*\angleindrop+180}{\refractedangle}
{\arcradius}
\end{scope}
% Draw the arcs of the angles of the rays leaving the raindrop. Note
% that the angles are identical to the original angle of incidence.
\drawarcdelta{(A'')}{\incidentangle+2*\angleindrop}{\incidentangle}
{\arcradius-1pt}
\drawarcdelta{(A'')}{\incidentangle+2*\angleindrop}{\incidentangle}
{\arcradius+1pt}
}
% Mark the center of the raindrop
\draw[fill] (O) circle (1.5pt);
\end{tikzpicture}
\end{document}
Click to download: raindrop.tex • raindrop.pdf
Open in Overleaf: raindrop.tex