This example shows using macros for drawing Karnaugh diagrams. They visualize boolean algebra expressions.
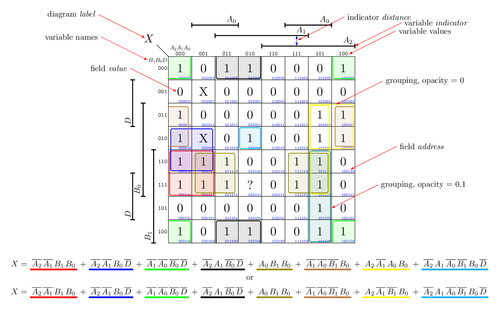
Edit and compile if you like:
% Karnaugh diagram
% Author: Uwe Zimmermann
\documentclass[x11names,border=10pt,tikz]{standalone}
\usepackage{xstring} % needed for string manipulations
\usepackage{fmtcount} % needed for some binary printing
\usetikzlibrary{calc,math}
\newif\ifKaddress
\newif\ifKInd
\pgfkeys{
/K/.is family, /K,
x bits/.estore in = \KXvars, % bits along the horizontal axis
y bits/.estore in = \KYvars, % bits along the vertical axis
variable names/.estore in = \KVars, % comma-separated variable names
label/.estore in = \KLabel, % label for the diagram
label scale/.estore in = \KLabelscale,% scale factor for values
value scale/.estore in = \KValscale, % scale factor for values
variable scale/.estore in = \KVarscale, % scale factor for variables
variable sep/.estore in = \KVarsep, % inner sep for variables
address scale/.estore in = \KAddrscale, % scale factor for adresses
address sep/.estore in = \KAddrsep, % inner sep for adresses
group distance/.estore in = \KGdist, % distance for grouping lines
group color/.estore in = \KGcolor, % grouping color
group linewidth/.estore in = \KGwidth, % grouping line width
group rounded/.estore in = \KGrounded, % grouping rounded corner radius
group opacity/.estore in = \KGopacity, % grouping field opacity
indicator distance/.estore in = \KInddist, % variable indicator distance
indicator linewidth/.estore in = \KIndwidth, % line width for indicators
indicator scale/.estore in = \KIndscale, % scale factor for indicators
indicator sep/.estore in = \KIndsep, % inner sep for indicators
plot addresses/.is if=Kaddress, % plot address fields
plot indicators/.is if=KInd, % plot variable indicators
}
\pgfkeys{
/K,
default/.style = { plot addresses = true,
plot indicators = true,
x bits = 2,
y bits = 2,
address scale = 0.5,
address sep = 1pt,
variable names = {$A$,$B$,$C$,$D$,$E$,$F$,$G$},
label = $X$,
label scale = 1.4,
variable scale = 0.7,
variable sep = 2pt,
value scale = 1.5,
group color = red,
group rounded = 2pt,
group linewidth = .3mm,
group opacity = 0.10,
group distance = 0.4,
indicator distance = 0.45,
indicator linewidth = .4mm,
indicator scale = 1.0,
indicator sep = 2pt,
}
}
\tikzset{
Kcorners/.style = { rounded corners = \KGrounded },
Kline/.style = { Kcorners, draw = \KGcolor, line width = \KGwidth },
KInd/.style = { draw = black, line width = \KIndwidth },
Kfill/.style = { Kcorners, fill = \KGcolor, opacity = \KGopacity },
Krect/.style = { Kcorners, Kfill },
right/.style = { black, anchor = west }, % nodes at right side
left/.style = { black, anchor = east }, % nodes at left side
}
\let\ol\overline% just to abbreviate
%==============================================================================
% K[options]{table}
%
% takes the address,value pairs from the comma-separated list {table} and
% draws up the corresponding K diagram.
% the table does not need to be sorted, nor to be complete
%
\newcommand{\K}[2][]
{%
\pgfkeys{/K, default, #1}%
\def\newstr{#2}
\tikzmath
{
function fromgray(\gcode,\bits) %
{
int \x, \pos, \leftbit, \twop;
\leftbit = 0;
\pos = 0;
for \x in {0,...,\bits-1}%
{
\twop = 2^(\bits - \x -1);
if \gcode >= \twop then %
{ % gray code is 1
if \leftbit == 0 then %
{
\pos = \pos + \twop;
\leftbit = 1;
} else
{
\leftbit = 0;
};
\gcode = \gcode - \twop;
} else
{ % gray code is 0
if \leftbit == 0 then %
{
\pos = \pos;
} else
{
\pos = \pos + \twop;
\leftbit = 1;
};
};
};
return \pos;
};
%
int \xbits, \ybits, \fields, \vars;
\xbits = \KXvars;
\ybits = \KYvars;
\vars = \xbits+\ybits;
\fields = 2^(\vars);
}
\StrCut[\xbits]{\KVars}{,}{\xlabels}{\ylabels}
\StrBefore[\ybits]{\ylabels}{,}[\ylabels]
\StrSubstitute[0]{\xlabels}{,}{}[\xlabels]
\StrSubstitute[0]{\ylabels}{,}{}[\ylabels]
\path ($(0,0.5)+\KVarscale*(0,2ex)$) node[anchor = south,
inner sep = \KVarsep, scale = \KVarscale] {\ttfamily\xlabels};
\path (-0.5,0.5) node[anchor = north east,
inner sep = \KVarsep, scale = \KVarscale] {\ttfamily\ylabels};
\foreach [remember = \newstr as \workstr (initially \newstr)]
\i in {1,...,\fields} {%
\StrCut[2]{\workstr}{,}{\nowstr}{\newstr}
\StrLen{\newstr}[\len]
\ifthenelse{\equal{\len}{0}}{\def\newstr{,,}}{}%
\StrLen{\nowstr}[\len]
\ifthenelse{\equal{\len}{1}}{}%
{%
\StrCut[1]{\nowstr}{,}{\addrstr}{\valuestr}
\tikzmath{
int \xpos, \ypos, \xaddr, \yaddr, \addr;
\addr = 0b\addrstr;
\xaddr = int(\addr / 2^\ybits);
\yaddr = \addr - \xaddr * 2^\ybits;
\xpos = fromgray(\xaddr,\xbits);
\ypos = fromgray(\yaddr,\ybits);
} % end tikzmath
% place field value
\path ($(\xpos,-\ypos)$) node[anchor=center,
inner sep = 0pt, scale = \KValscale](F\addrstr){\valuestr};
}%
}
\tikzmath
{
int \x, \y, \xmax, \ymax, \value;
\xmax = 2^\xbits - 1;
\ymax = 2^\ybits - 1;
{ \draw ($(-0.5,0.5)$) -- ($(-0.5,-\ymax-0.5)$); };
for \x in {0,...,\xmax}%
{
\xpos = fromgray(\x,\xbits);
{
\path ($(\xpos,0.5)$) node[anchor = south, black, inner sep = 2pt,
scale = \KVarscale]{\ttfamily\padzeroes[\xbits]\binarynum{\x}};
\draw ($(\xpos+0.5,0.5)$) -- ($(\xpos+0.5,-\ymax-0.5)$);
};
};
{ \draw ($(-0.5,+0.5)$) -- ($(\xmax+0.5,+0.5)$); };
for \y in {0,...,\ymax}%
{
\ypos = fromgray(\y,\ybits);
{
\path ($(-0.5,-\ypos)$) node[anchor=east, black, inner sep = 2pt,
scale = \KVarscale] {\ttfamily\padzeroes[\ybits]\binarynum{\y}};
\draw ($(-0.5,-\ypos-0.5)$) -- ($(\xmax+0.5,-\ypos-0.5)$);
};
};
}
\ifKaddress
\tikzmath
{
int \x, \y, \xmax, \ymax, \value;
\xmax = 2^\xbits - 1;
\ymax = 2^\ybits - 1;
for \x in {0,...,\xmax}%
{
\xpos = fromgray(\x,\xbits);
for \y in {0,...,\ymax}%
{
\ypos = fromgray(\y,\ybits);
{ %
\path ($(\xpos,-\ypos)+(0.5,-0.5)$) node[anchor = south east,
inner sep = \KAddrsep, blue, scale = \KAddrscale]
{\ttfamily\padzeroes[\xbits]%
\binarynum{\x}\padzeroes[\ybits]\binarynum{\y}};
};
};
};
}
\fi
\ifKInd
\tikzmath%
{%
int \i, \il, \j, \n;
real \x,\xmax,\y,\ymax;
for \i in {1,...,\xbits}%
{
\n = 2^(\i-2);
\il = \i+1;
if \n < 1 then {\n=1;};
\y = 0.5 + \KInddist*(\i);
for \j in {1,...,\n}%
{
\x = -0.5 + 2^(\xbits-\i) + (\j-1)*2^(\xbits-\i+2);
\xmax = \x + 2^(\xbits-\i+1);
if \xmax > (2^(\xbits)-0.5) then {\xmax=2^(\xbits)-0.5;};
{
\StrBetween[\i,\numexpr\i+1]{,\KVars,}{,}{,}[\tlabel]
\path [KInd] (\x,\y) -- (\xmax,\y) node[anchor = south east,
inner sep = \KIndsep, scale = \KIndscale] {\tlabel};
\path [KInd] (\x,\y)++(0,-0.1) -- ++(0,+0.2);
\path [KInd] (\xmax,\y)++(0,-0.1) -- ++(0,+0.2);
};
};
};
for \i in {1,...,\ybits}%
{
\n = 2^(\i-2);
if \n < 1 then {\n=1;};
\x = -0.5 - \KInddist*(\i-1);
for \j in {1,...,\n}%
{
\y = -0.5 + 2^(\ybits-\i) + (\j-1)*2^(\ybits-\i+2);
\ymax = \y + 2^(\ybits-\i+1);
if \ymax > (2^(\ybits)-0.5) then {\ymax=2^(\ybits)-0.5;};
{
\StrBetween[\numexpr\i+\xbits,\numexpr\i+\xbits+1]
{,\KVars,}{,}{,}[\tlabel]
\path [KInd] ($(\x,-\y)-\ybits*(1.4ex,0)$)
-- ($(\x,-\ymax)-\ybits*(1.4ex,0)$) node[anchor=south west,
rotate=90, inner sep=\KIndsep, scale=\KIndscale]{\tlabel};
\path [KInd] ($(\x,-\y)-\ybits*(1.4ex,0)$)++(-0.1,0) -- ++(+0.2,0);
\path [KInd] ($(\x,-\ymax)-\ybits*(1.4ex,0)$)++(-0.1,0) -- ++(+0.2,0);
};
};
};
}
\fi
\path[draw = black] (-0.5,0.5) -- ++(-0.5,0.5) node[anchor = south east,
inner sep = 2pt, scale = \KLabelscale] {\KLabel};
}
%==============================================================================
% KG[options]{from}{to}
%
% groups together the fields between {from} and {to} by drawing a frame around
% these fields.
% if the {from} field is above or right of the {to} field, the frame is
% extended around the edge of the diagram.
%
\newcommand{\KG}[3][] % options from to
{%
\pgfkeys{/K, default, #1}%
\tikzmath
{
int \xbits, \ybits, \fields, \vars;
\xbits = \KXvars;
\ybits = \KYvars;
\vars = \xbits+\ybits;
\fields = 2^(\vars);
}
\tikzmath{
int \xfrompos, \yfrompos, \xfrom, \yfrom, \fromaddr;
int \xtopos, \ytopos, \xto, \yto, \toaddr;
\fromaddr = 0b#2;
\toaddr = 0b#3;
\xfrom = int(\fromaddr / 2^\ybits);
\yfrom = \fromaddr - \xfrom * 2^\ybits;
\xto = int(\toaddr / 2^\ybits);
\yto = \toaddr - \xto * 2^\ybits;
\xfrompos = fromgray(\xfrom,\xbits);
\yfrompos = fromgray(\yfrom,\ybits);
\xtopos = fromgray(\xto,\xbits);
\ytopos = fromgray(\yto,\ybits);
\xmax = 2^\xbits-1;
\ymax = 2^\ybits-1;
} % end tikzmath
\tikzmath%
{
if (\xfrompos <= \xtopos) && (\yfrompos >= \ytopos) then %
{
{
\path[Kfill] ($(\xfrompos,-\yfrompos)-(\KGdist,\KGdist)$)
rectangle ($(\xtopos,-\ytopos)+(\KGdist,\KGdist)$);
\path[Kline] ($(\xfrompos,-\yfrompos)-(\KGdist,\KGdist)$)
rectangle ($(\xtopos,-\ytopos)+(\KGdist,\KGdist)$);
};
};
if (\xfrompos <= \xtopos) && (\yfrompos < \ytopos) then %
{
{
\path[Krect] ($(\xfrompos,0)+(-\KGdist,+0.5)$)
-- ($(\xfrompos,-\yfrompos)+(-\KGdist,-\KGdist)$)
-- ($(\xtopos,-\yfrompos)+(\KGdist,-\KGdist)$)
-- ($(\xtopos,0)+(\KGdist,+0.5)$) -- cycle;
\path[Krect] ($(\xfrompos,-\ymax)+(-\KGdist,-0.5)$)
-- ($(\xfrompos,-\ytopos)+(-\KGdist,+\KGdist)$)
-- ($(\xtopos,-\ytopos)+(\KGdist,+\KGdist)$)
-- ($(\xtopos,-\ymax)+(\KGdist,-0.5)$) -- cycle;
\path[Kline] ($(\xfrompos,0)+(-\KGdist,+0.5)$)
-- ($(\xfrompos,-\yfrompos)+(-\KGdist,-\KGdist)$)
-- ($(\xtopos,-\yfrompos)+(\KGdist,-\KGdist)$)
-- ($(\xtopos,0)+(\KGdist,+0.5)$);
\path[Kline] ($(\xfrompos,-\ymax)+(-\KGdist,-0.5)$)
-- ($(\xfrompos,-\ytopos)+(-\KGdist,+\KGdist)$)
-- ($(\xtopos,-\ytopos)+(\KGdist,+\KGdist)$)
-- ($(\xtopos,-\ymax)+(\KGdist,-0.5)$);
};
};
if (\xfrompos > \xtopos) && (\yfrompos >= \ytopos) then %
{
{
\path[Krect] ($(0,-\yfrompos)+(-0.5,-\KGdist)$)
-- ($(\xtopos,-\yfrompos)+(+\KGdist,-\KGdist)$)
-- ($(\xtopos,-\ytopos)+(\KGdist,+\KGdist)$)
-- ($(0,-\ytopos)+(-0.5,+\KGdist)$) -- cycle;
\path[Krect] ($(\xmax,-\yfrompos)+(+0.5,-\KGdist)$)
-- ($(\xfrompos,-\yfrompos)+(-\KGdist,-\KGdist)$)
-- ($(\xfrompos,-\ytopos)+(-\KGdist,+\KGdist)$)
-- ($(\xmax,-\ytopos)+(+0.5,+\KGdist)$) -- cycle;
\path[Kline] ($(0,-\yfrompos)+(-0.5,-\KGdist)$)
-- ($(\xtopos,-\yfrompos)+(+\KGdist,-\KGdist)$)
-- ($(\xtopos,-\ytopos)+(\KGdist,+\KGdist)$)
-- ($(0,-\ytopos)+(-0.5,+\KGdist)$);
\path[Kline] ($(\xmax,-\yfrompos)+(+0.5,-\KGdist)$)
-- ($(\xfrompos,-\yfrompos)+(-\KGdist,-\KGdist)$)
-- ($(\xfrompos,-\ytopos)+(-\KGdist,+\KGdist)$)
-- ($(\xmax,-\ytopos)+(+0.5,+\KGdist)$);
};
};
if (\xfrompos > \xtopos) && (\yfrompos < \ytopos) then %
{
{
\path[Kfill] {[Kcorners] ($(0,-\yfrompos)+(-0.5,-\KGdist)$)
-- ($(\xtopos,-\yfrompos)+(+\KGdist,-\KGdist)$)
-- ($(\xtopos,0)+(\KGdist,+0.5)$)}
-- ($(0,0)+(-0.5,+0.5)$) -- cycle;
\path[Kfill] {[Kcorners] ($(0,-\ytopos)+(-0.5,+\KGdist)$)
-- ($(\xtopos,-\ytopos)+(+\KGdist,+\KGdist)$)
-- ($(\xtopos,-\ymax)+(\KGdist,-0.5)$)}
-- ($(0,-\ymax)+(-0.5,-0.5)$) -- cycle;
\path[Kfill] {[Kcorners] ($(\xmax,-\yfrompos)+(+0.5,-\KGdist)$)
-- ($(\xfrompos,-\yfrompos)+(-\KGdist,-\KGdist)$)
-- ($(\xfrompos,0)+(-\KGdist,+0.5)$)}
-- ($(\xmax,0)+(+0.5,+0.5)$) -- cycle;
\path[Kfill] {[Kcorners] ($(\xmax,-\ytopos)+(+0.5,+\KGdist)$)
-- ($(\xfrompos,-\ytopos)+(-\KGdist,+\KGdist)$)
-- ($(\xfrompos,-\ymax)+(-\KGdist,-0.5)$)}
-- ($(\xmax,-\ymax)+(+0.5,-0.5)$) -- cycle;
\path[Kline] ($(0,-\yfrompos)+(-0.5,-\KGdist)$)
-- ($(\xtopos,-\yfrompos)+(+\KGdist,-\KGdist)$)
-- ($(\xtopos,0)+(\KGdist,+0.5)$);
\path[Kline] ($(0,-\ytopos)+(-0.5,+\KGdist)$)
-- ($(\xtopos,-\ytopos)+(+\KGdist,+\KGdist)$)
-- ($(\xtopos,-\ymax)+(\KGdist,-0.5)$);
\path[Kline] ($(\xmax,-\yfrompos)+(+0.5,-\KGdist)$)
-- ($(\xfrompos,-\yfrompos)+(-\KGdist,-\KGdist)$)
-- ($(\xfrompos,0)+(-\KGdist,+0.5)$);
\path[Kline] ($(\xmax,-\ytopos)+(+0.5,+\KGdist)$)
-- ($(\xfrompos,-\ytopos)+(-\KGdist,+\KGdist)$)
-- ($(\xfrompos,-\ymax)+(-\KGdist,-0.5)$);
};
};
}
}
\newcommand*\ul[2]{\tikz[baseline = (char.base)]{
\node[inner sep = 2pt] (char) {#2};
\draw[#1, line width = 2pt](char.south west) -- (char.south east);}}
\begin{document}
\begin{tikzpicture}[x=1cm,y=1cm]
\K[x bits = 3, y bits = 3,
variable names = {$A_2$,$A_1$,$A_0$,$B_1$,$B_0$,$D$,}]
{ % some random truth table...
000000,1, 010000,1, 100000,1, 110000,0,
000001,0, 010001,0, 100001,0, 110001,0,
000010,1, 010010,1, 100010,1, 110010,0,
000011,1, 010011,0, 100011,1, 110011,0,
000100,1, 010100,1, 100100,1, 110100,0,
000101,0, 010101,0, 100101,0, 110101,0,
000110,1, 010110,0, 100110,0, 110110,0,
000111,1, 010111,?, 100111,0, 110111,0,
001000,0, 011000,1, 101000,0, 111000,0,
001001,X, 011001,0, 101001,0, 111001,0,
001010,X, 011010,0, 101010,1, 111010,0,
001011,0, 011011,0, 101011,1, 111011,0,
001100,0, 011100,1, 101100,1, 111100,0,
001101,0, 011101,0, 101101,1, 111101,0,
001110,1, 011110,1, 101110,1, 111110,1,
001111,1, 011111,1, 101111,1, 111111,1,
}
\newcommand*{\myKG}[4][0.1]{\KG[x bits = 3,y bits = 3,group opacity = #1,
#2]{#3}{#4}}
\myKG {group color = green, group distance=0.45}{100000}{000100}
\myKG {group color = red, group distance=0.45}{000111}{001110}
\myKG {group color = blue, group distance=0.40}{000110}{001010}
\myKG {group color = olive, group distance=0.35}{001111}{011110}
\myKG {group color = olive, group distance=0.35}{111111}{101110}
\myKG {group color = brown, group distance=0.35}{100010}{000011}
\myKG {group color = black, group distance=0.45}{011000}{010100}
\myKG {group color = cyan, group distance=0.45}{010010}{010010}
\myKG {group color = teal, group distance=0.45}{101100}{101110}
\myKG[0.0]{group color = yellow, group distance=0.40}{101111}{101011}
\myKG[0.0]{group color = yellow, group distance=0.45}{101010}{100011}
%=====================================================================
% in picture comments
%=====================================================================
\begin{scope}[latex-,red]
\draw (6.7,-1.55) -- ++(2,1) node[right] {grouping, opacity = 0};
\draw (6.5,-6.0) -- ++(2,1) node[right] {grouping, opacity = 0.1};
\draw (7.5,+0.95) -- ++(2,1) node[right] {variable \emph{indicator}};
\draw (7.3,-4.35) -- ++(2,1) node[right] {field \emph{address}};
\draw (7.25,+0.6) -- ++(2,1) node[right] {variable values};
\draw (-1.5,+1.3) -- ++(-2,1) node[left] {diagram \emph{label}};
\draw (-1.4,+0.35) -- ++(-2,1) node[left] {variable names};
\draw (-0.15,-1.0) -- ++(-2,1) node[left] {field \emph{value}};
\draw (5.05,1.2) -- ++(2,1) node[right] {indicator \emph{distance}};
\end{scope}
\draw [latex-latex,blue] (5,0.95) -- ++(0,0.45);
\path (3,-8) node[anchor = north, align = left] (eq1){%
$X =
\ul{red}{$\ol{A_2}\,\ol{A_1}\,B_1\,B_0$}
+\ul{blue}{$\ol{A_2}\,\ol{A_1}\,B_0\,\ol{D}$}
+\ul{green}{$\ol{A_1}\,\ol{A_0}\,\ol{B_0}\,\ol{D}$}
+\ul{black}{$\ol{A_2}\,A_1\,\ol{B_0}\,\ol{D}$}
+\ul{olive}{$A_0\,{B_1}\,{B_0}$}
+\ul{brown}{$\ol{A_1}\,\ol{A_0}\,\ol{B_1}\,{B_0}$}
+\ul{yellow}{${A_2}\,\ol{A_1}\,{A_0}\,{B_0}$}
+\ul{cyan}{$\ol{A_2}\,{A_1}\,\ol{A_0}\,\ol{B_1}\,{B_0}\,\ol{D}$}
$};
\path(eq1.south) node[anchor = north] (t1) {or};
\path (t1.south) node[anchor = north, align = left] (eq2){%
$X =
\ul{red}{$\ol{A_2}\,\ol{A_1}\,B_1\,B_0$}
+\ul{blue}{$\ol{A_2}\,\ol{A_1}\,B_0\,\ol{D}$}
+\ul{green}{$\ol{A_1}\,\ol{A_0}\,\ol{B_0}\,\ol{D}$}
+\ul{black}{$\ol{A_2}\,A_1\,\ol{B_0}\,\ol{D}$}
+\ul{olive}{$A_0\,{B_1}\,{B_0}$}
+\ul{brown}{$\ol{A_1}\,\ol{A_0}\,\ol{B_1}\,{B_0}$}
+\ul{yellow}{${A_2}\,\ol{A_1}\,\ol{B_1}\,{B_0}$}
+\ul{cyan}{$\ol{A_2}\,{A_1}\,\ol{A_0}\,\ol{B_1}\,{B_0}\,\ol{D}$}
$};
\end{tikzpicture}
\end{document}
Click to download: karnaugh-diagram.tex • karnaugh-diagram.pdf
Open in Overleaf: karnaugh-diagram.tex


