Example: A hexagon for memorizing trigonometric identities

Published 2012-01-06 | Author: Josef Nilsen

Download as: [PDF] [TEX]

A hexagon for memorizing trigonometric identities

Do you have a question regarding this example, TikZ or LaTeX in general? Just ask in the LaTeX Forum.
Oder frag auf Deutsch auf TeXwelt.de. En français: TeXnique.fr.

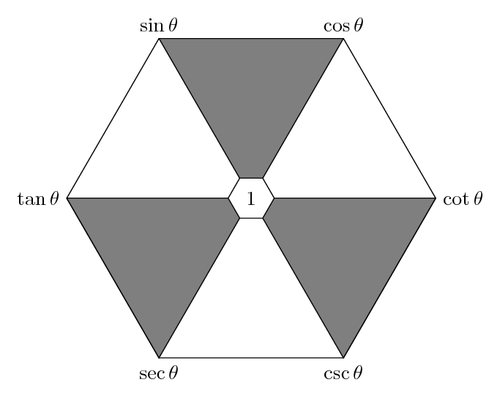
% A hexagon for memorizing trigonometric identities
% Author: Josef Nilsen
\documentclass{article}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}[scale=4,cap=round,>=latex]
% Radius of regular polygons
  \newdimen\R
  \R=0.8cm
  \coordinate (center) at (0,0);
 \draw (0:\R)
     \foreach \x in {60,120,...,360} {  -- (\x:\R) }
              -- cycle (300:\R) node[below] {$\csc \theta$}
              -- cycle (240:\R) node[below] {$\sec \theta$}
              -- cycle (180:\R) node[left] {$\tan \theta$}
              -- cycle (120:\R) node[above] {$\sin \theta$}
              -- cycle (60:\R) node[above] {$\cos \theta$}
              -- cycle (0:\R) node[right] {$\cot \theta$};
  \draw { (60:\R) -- (120:\R) -- (center) -- (60:\R) } [fill=gray];
  \draw { (180:\R) -- (240:\R) -- (center) -- (180:\R) } [fill=gray];
  \draw { (0:\R) -- (300:\R) -- (center) -- (0:\R) }  [fill=gray];
   \R=0.1cm
  \draw (0:\R) \foreach \x in {60,120,...,360} { -- (\x:\R) }
    [fill=white] -- cycle (center) node {1};
\end{tikzpicture}
\end{document}

Comments

#1 Jimi Oke, January 7, 2012 at 8:24 p.m.

Hi Josef,

Thanks for this example. Could you please explain how this example is used as a mnemonic? It might be helpful for my students.

Thanks, Jimi
#2 Josef Nilsen, January 12, 2012 at 10:29 p.m.

No problem! Just Google something like "trigonometric identities hexagon" without the quotes and you'll get plenty of results explaining it. Some examples:

http://mrsberryprecalculus.edublogs.org/files/2009/02/basictrigidentities2.pdf

http://www.casme.org.za/docs/The%20Hexagon%20Trig%20Trick2.pdf
#3 Jimi Oke, January 23, 2012 at 1:30 a.m.

Thanks! I was able to see how it could relate to the reciprocal and Pythagorean identities. But I'll follow the links you provided.

Thanks!