Illustration of how to compute the product of two matrices.
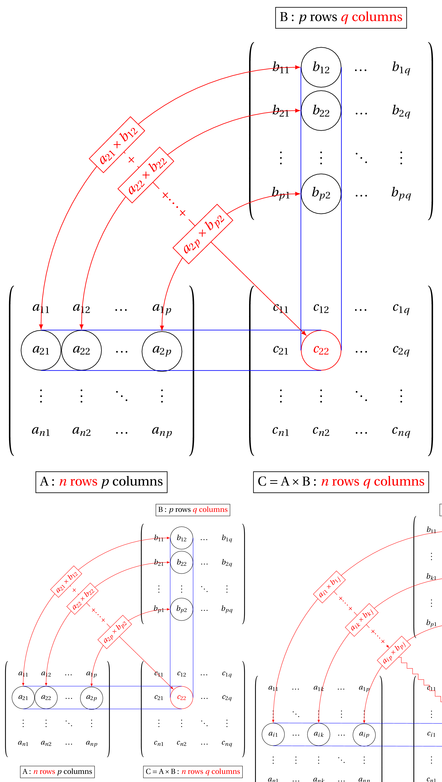
Edit and compile if you like:
% Author : Alain Matthes
% Source : http://altermundus.com/pages/examples.html
\documentclass[]{article}
\usepackage[utf8]{inputenc}
\usepackage[upright]{fourier}
\usepackage{tikz}
\usetikzlibrary{matrix,arrows,decorations.pathmorphing}
\begin{document}
% l' unite
\newcommand{\myunit}{1 cm}
\tikzset{
node style sp/.style={draw,circle,minimum size=\myunit},
node style ge/.style={circle,minimum size=\myunit},
arrow style mul/.style={draw,sloped,midway,fill=white},
arrow style plus/.style={midway,sloped,fill=white},
}
\begin{tikzpicture}[>=latex]
% les matrices
\matrix (A) [matrix of math nodes,
nodes = {node style ge},
left delimiter = (,
right delimiter = )] at (0,0)
{
a_{11} & a_{12} & \ldots & a_{1p} \\
|[node style sp]| a_{21}
& |[node style sp]| a_{22}
& \ldots
& |[node style sp]| a_{2p} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \ldots & a_{np} \\
};
\node [draw,below=10pt] at (A.south)
{ $A$ : \textcolor{red}{$n$ rows} $p$ columns};
\matrix (B) [matrix of math nodes,
nodes = {node style ge},
left delimiter = (,
right delimiter = )] at (6*\myunit,6*\myunit)
{
b_{11} & |[node style sp]| b_{12}
& \ldots & b_{1q} \\
b_{21} & |[node style sp]| b_{22}
& \ldots & b_{2q} \\
\vdots & \vdots & \ddots & \vdots \\
b_{p1} & |[node style sp]| b_{p2}
& \ldots & b_{pq} \\
};
\node [draw,above=10pt] at (B.north)
{ $B$ : $p$ rows \textcolor{red}{$q$ columns}};
% matrice résultat
\matrix (C) [matrix of math nodes,
nodes = {node style ge},
left delimiter = (,
right delimiter = )] at (6*\myunit,0)
{
c_{11} & c_{12} & \ldots & c_{1q} \\
c_{21} & |[node style sp,red]| c_{22}
& \ldots & c_{2q} \\
\vdots & \vdots & \ddots & \vdots \\
c_{n1} & c_{n2} & \ldots & c_{nq} \\
};
% les fleches
\draw[blue] (A-2-1.north) -- (C-2-2.north);
\draw[blue] (A-2-1.south) -- (C-2-2.south);
\draw[blue] (B-1-2.west) -- (C-2-2.west);
\draw[blue] (B-1-2.east) -- (C-2-2.east);
\draw[<->,red](A-2-1) to[in=180,out=90]
node[arrow style mul] (x) {$a_{21}\times b_{12}$} (B-1-2);
\draw[<->,red](A-2-2) to[in=180,out=90]
node[arrow style mul] (y) {$a_{22}\times b_{22}$} (B-2-2);
\draw[<->,red](A-2-4) to[in=180,out=90]
node[arrow style mul] (z) {$a_{2p}\times b_{p2}$} (B-4-2);
\draw[red,->] (x) to node[arrow style plus] {$+$} (y)%
to node[arrow style plus] {$+\raisebox{.5ex}{\ldots}+$} (z)
to (C-2-2.north west);
\node [draw,below=10pt] at (C.south)
{$ C=A\times B$ : \textcolor{red}{$n$ rows}
\textcolor{red}{$q$ columns}};
\end{tikzpicture}
\begin{tikzpicture}[>=latex]
% unit
% defintion of matrices
\matrix (A) [matrix of math nodes,%
nodes = {node style ge},%
left delimiter = (,%
right delimiter = )] at (0,0)
{%
a_{11} &\ldots & a_{1k} & \ldots & a_{1p} \\
\vdots & \ddots & \vdots & \vdots & \vdots \\
|[node style sp]| a_{i1} & \ldots%
& |[node style sp]| a_{ik}%
& \ldots%
& |[node style sp]| a_{ip} \\
\vdots & \vdots& \vdots & \ddots & \vdots \\
a_{n1}& \ldots & a_{nk} & \ldots & a_{np} \\
};
\node [draw,below] at (A.south)
{ $A$ : \textcolor{red}{$n$ rows} $p$ columns};
\matrix (B) [matrix of math nodes,%
nodes = {node style ge},%
left delimiter = (,%
right delimiter =)] at (7*\myunit,7*\myunit)
{%
b_{11} & \ldots& |[node style sp]| b_{1j}%
& \ldots & b_{1q} \\
\vdots& \ddots & \vdots & \vdots & \vdots \\
b_{k1} & \ldots& |[node style sp]| b_{kj}%
& \ldots & b_{kq} \\
\vdots& \vdots & \vdots & \ddots & \vdots \\
b_{p1} & \ldots& |[node style sp]| b_{pj}%
& \ldots & b_{pq} \\
};
\node [draw,above] at (B.north)
{ $B$ : $p$ rows \textcolor{red}{$q$ columns}};
% matrice resultat
\matrix (C) [matrix of math nodes,%
nodes = {node style ge},%
left delimiter = (,%
right delimiter = )] at (7*\myunit,0)
{%
c_{11} & \ldots& c_{1j} & \ldots & c_{1q} \\
\vdots& \ddots & \vdots & \vdots & \vdots \\
c_{i1}& \ldots & |[node style sp,red]| c_{ij}%
& \ldots & c_{iq} \\
\vdots& \vdots & \vdots & \ddots & \vdots \\
c_{n1}& \ldots & c_{nk} & \ldots & c_{nq} \\
};
\node [draw,below] at (C.south)
{$ C=A\times B$ : \textcolor{red}{$n$ rows}
\textcolor{red}{$q$ columns}};
% arrows
\draw[blue] (A-3-1.north) -- (C-3-3.north);
\draw[blue] (A-3-1.south) -- (C-3-3.south);
\draw[blue] (B-1-3.west) -- (C-3-3.west);
\draw[blue] (B-1-3.east) -- (C-3-3.east);
\draw[<->,red](A-3-1) to[in=180,out=90]
node[arrow style mul] (x) {$a_{i1}\times b_{1j}$} (B-1-3);
\draw[<->,red](A-3-3) to[in=180,out=90]
node[arrow style mul] (y) {$a_{ik}\times b_{kj}$}(B-3-3);
\draw[<->,red](A-3-5) to[in=180,out=90]
node[arrow style mul] (z) {$a_{ip}\times b_{pj}$}(B-5-3);
\draw[red,->] (x) to node[arrow style plus] {$+\raisebox{.5ex}{\ldots}+$} (y)
to node[arrow style plus] {$+\raisebox{.5ex}{\ldots}+$} (z);
%
% to (C-3-3.north west);
\draw[->,red,decorate,decoration=zigzag] (z) -- (C-3-3.north west);
\end{tikzpicture}
\end{document}
% encoding : utf8
% format : pdfLaTeX
% author : Alain Matthes
Click to download: matrix-multiplication.tex • matrix-multiplication.pdf
Open in Overleaf: matrix-multiplication.tex


