Rotation of the sphere in 3D

This is a drawing using tikz-3dplot package. The original is from the Nagoya University entrance exam question of 2025.

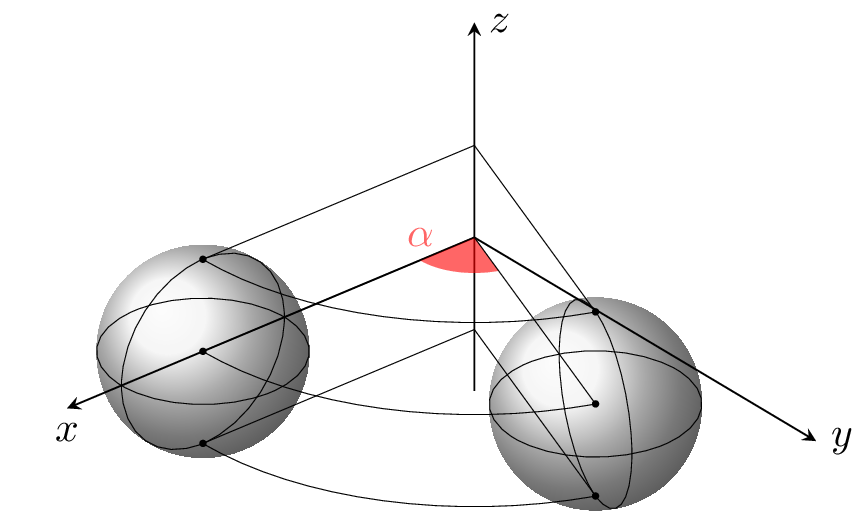
Edit and compile if you like:

\documentclass{standalone}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{calc,backgrounds}

\begin{document}
\tdplotsetmaincoords{60}{140}
\begin{tikzpicture}[
    tdplot_main_coords,
    scale=3,
    axis/.style={-stealth},
    addline/.style={very thin}
]

    \begin{scope}[axis]
        \draw (0,0,0) -- (1.5,0,0) node[below]{$x$};
        \draw (0,0,0) -- (0,1.5,0) node[right]{$y$};
        \draw (0,0,-0.5) -- (0,0,0.7) node[right]{$z$};
    \end{scope}

    \def\r{0.3} % radius of sphere
    \def\a{70} % rotation angle

    \coordinate (A) at (1,0,0);
    \coordinate (B) at ({cos(\a)},{sin(\a)},0);
    \foreach \P/\Ptop/\Pbottom in {A/Atop/Abottom, B/Btop/Bbottom} {
        \coordinate (\Ptop) at ($(\P)+(0,0,\r)$);
        \coordinate (\Pbottom) at ($(\P)+(0,0,-\r)$);
    }

    % rotation angle
    \fill[red, opacity=0.6] (0.2,0) node[above]{$\alpha$} 
        arc [radius=0.2, start angle=0, end angle=\a] -- (0,0,0) -- cycle;

    % draw additional line
    \begin{scope}[addline]
        \draw (A) circle (\r);
        \draw (B) circle (\r);
        \foreach \h in {-\r,0,\r}
            \draw (1,0,\h) arc [radius=1, start angle=0, end angle=\a] -- (0,0,\h) -- cycle;
        
        \tdplotsetrotatedcoords{\a-90}{90}{0}
        \tdplotdrawarc[tdplot_rotated_coords]{(B)}{\r}{0}{360}{}{}
        
        \tdplotsetrotatedcoords{90}{90}{0}
        \tdplotdrawarc[tdplot_rotated_coords]{(A)}{\r}{0}{360}{}{}
    \end{scope}

    %point and sphere
    \begin{scope}[tdplot_screen_coords, on background layer]
        \fill[ball color=lightgray!20!] (A) circle (\r); 
        \fill[ball color=lightgray!20!] (B) circle (\r); 
        \foreach \P in {A,B,Atop,Btop,Abottom,Bbottom}
            \fill (\P) circle (0.01);
    \end{scope}
\end{tikzpicture}
\end{document}