Logarithmic spiral

A logarithmic spiral.

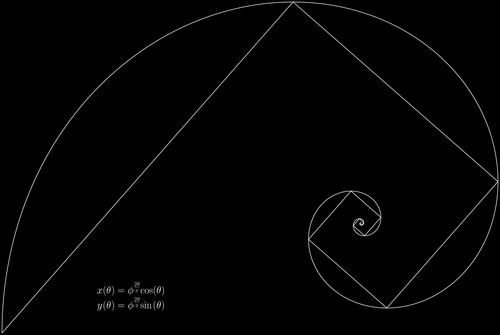
Edit and compile if you like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
% Logarithmic spiral
% Author: Andrew Mertz
\documentclass{minimal}
\usepackage{tikz}
\usetikzlibrary{backgrounds,calc}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{0pt}%
\begin{document}
\begin{tikzpicture}[background rectangle/.style={fill=black},
                    show background rectangle, x=1pt, y=1pt]
 % Compute the golden ratio
  \pgfmathsetmacro{\goldenRatio}{(1+sqrt(5)) / 2}
  % Compute the angle between the tangent and radial line 
  \pgfmathsetmacro{\offset}{rad(atan(2*ln(\goldenRatio)/pi))};
  % Plot the spiral using the parametric form of a logarithmic spiral
  % (a e^{b t} cos(t), a e^{b t} sin(t)). In this case a = 1 and b = 2
  % ln((1+sqrt(5)) / 2) / pi. There can be a slight gap between the
  % last line segment and the end of the plot. Having a large sample
  % size reduces the gap.
  \draw[very thick,white,domain=\offset:\offset+14*pi/2,
       smooth,samples=600,variable=\t] plot
   ({pow(\goldenRatio, 2 * \t / pi) * cos(\t r)},
    {pow(\goldenRatio, 2 * \t / pi) * sin(\t r)}) 
   coordinate(end);
  % Remember the start of the spiral
  \coordinate (0) at 
    ({pow(\goldenRatio, 2 * \offset / pi) * cos(\offset r)},
     {pow(\goldenRatio, 2 * \offset / pi) * sin(\offset r)});
 % This loop draws the line segments
  \foreach \i in {1,...,14}
  {
    % Get the "name" of the last point on the spiral
    \pgfmathsetmacro{\lastpoint}{\i-1}
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX