This example is from the tutorial: A picture for Karl's students.
Author: Till Tantau Source: The PGF/TikZ manual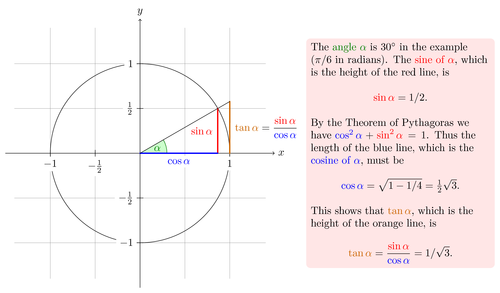
Edit and compile if you like:
% Author: Till Tantau
% Source: The PGF/TikZ manual
\documentclass{minimal}
\usepackage{tikz}
%\usetikzlibrary{trees,snakes}
\begin{document}
\pagestyle{empty}
\begin{tikzpicture}[scale=3,cap=round]
% Local definitions
\def\costhirty{0.8660256}
% Colors
\colorlet{anglecolor}{green!50!black}
\colorlet{sincolor}{red}
\colorlet{tancolor}{orange!80!black}
\colorlet{coscolor}{blue}
% Styles
\tikzstyle{axes}=[]
\tikzstyle{important line}=[very thick]
\tikzstyle{information text}=[rounded corners,fill=red!10,inner sep=1ex]
% The graphic
\draw[style=help lines,step=0.5cm] (-1.4,-1.4) grid (1.4,1.4);
\draw (0,0) circle (1cm);
\begin{scope}[style=axes]
\draw[->] (-1.5,0) -- (1.5,0) node[right] {$x$};
\draw[->] (0,-1.5) -- (0,1.5) node[above] {$y$};
\foreach \x/\xtext in {-1, -.5/-\frac{1}{2}, 1}
\draw[xshift=\x cm] (0pt,1pt) -- (0pt,-1pt) node[below,fill=white]
{$\xtext$};
\foreach \y/\ytext in {-1, -.5/-\frac{1}{2}, .5/\frac{1}{2}, 1}
\draw[yshift=\y cm] (1pt,0pt) -- (-1pt,0pt) node[left,fill=white]
{$\ytext$};
\end{scope}
\filldraw[fill=green!20,draw=anglecolor] (0,0) -- (3mm,0pt) arc(0:30:3mm);
\draw (15:2mm) node[anglecolor] {$\alpha$};
\draw[style=important line,sincolor]
(30:1cm) -- node[left=1pt,fill=white] {$\sin \alpha$} +(0,-.5);
\draw[style=important line,coscolor]
(0,0) -- node[below=2pt,fill=white] {$\cos \alpha$} (\costhirty,0);
\draw[style=important line,tancolor] (1,0) --
node [right=1pt,fill=white]
{
$\displaystyle \tan \alpha \color{black}=
\frac{{\color{sincolor}\sin \alpha}}{\color{coscolor}\cos \alpha}$
} (intersection of 0,0--30:1cm and 1,0--1,1) coordinate (t);
\draw (0,0) -- (t);
\draw[xshift=1.85cm] node [right,text width=6cm,style=information text]
{
The {\color{anglecolor} angle $\alpha$} is $30^\circ$ in the
example ($\pi/6$ in radians). The {\color{sincolor}sine of
$\alpha$}, which is the height of the red line, is
\[
{\color{sincolor} \sin \alpha} = 1/2.
\]
By the Theorem of Pythagoras we have ${\color{coscolor}\cos^2 \alpha} +
{\color{sincolor}\sin^2\alpha} =1$. Thus the length of the blue
line, which is the {\color{coscolor}cosine of $\alpha$}, must be
\[
{\color{coscolor}\cos\alpha} = \sqrt{1 - 1/4} = \textstyle
\frac{1}{2} \sqrt 3.
\]%
This shows that {\color{tancolor}$\tan \alpha$}, which is the
height of the orange line, is
\[
{\color{tancolor}\tan\alpha} = \frac{{\color{sincolor}\sin
\alpha}}{\color{coscolor}\cos \alpha} = 1/\sqrt 3.
\]%
};
\end{tikzpicture}
\end{document}Click to download: tutorial.tex • tutorial.pdf
Open in Overleaf: tutorial.tex