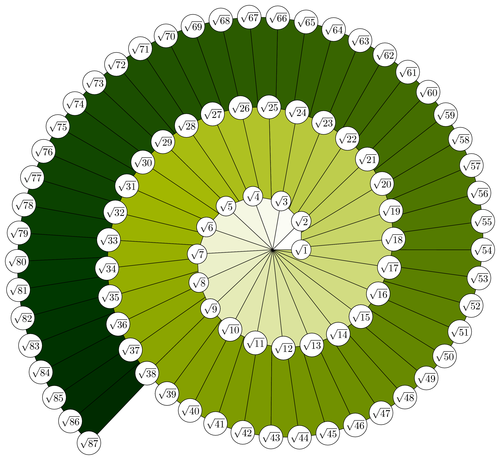
Example: Rooty helix

Published 2008-12-07 | Author: Felix Lindemann

The idea of the rooty-helix is very simple. One starts e.g. with the length of 1, adds a right angle with the length of 1 and the hypotenuse equals sqrt{2}. If one continues with sqrt{2} repeating the procedure (adding a right angle with the length of 1) the hypotenuse is sqrt{3}. And so on and so on. At some point due to the iterations some triangles are overpainted. Because of this, one repaints the overpainted triangles

Download as: [PDF] [TEX]

Do you have a question regarding this example, TikZ or LaTeX in general? Just ask in the LaTeX Forum.
Oder frag auf Deutsch auf TeXwelt.de. En français: TeXnique.fr.

% Rooty helix
% Author: Felix Lindemann
\documentclass{minimal}

\usepackage{tikz}
\usetikzlibrary{calc}
\begin{document}

\pagestyle{empty}
\pgfdeclarelayer{background}
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}

\xdefinecolor{darkgreen}{RGB}{175, 193, 36}
\newcounter{cntShader}
\newcounter{cntRoot}
\setcounter{cntShader}{20}
\def\couleur{darkgreen}

\begin{tikzpicture}
    \foreach \y in {86,38,15}{
        \setcounter{cntShader}{1}
        \coordinate (a) at (0,0);
        \coordinate (b) at (0:1);
        \foreach \x in {1,...,\y}{%
            \coordinate (c) at ($ (b)!1cm!270:(a) $);
            \begin{pgfonlayer}{background}
                \draw[fill=\couleur!\thecntShader] (a)--(b)--(c)--cycle;
            \end{pgfonlayer}
            \setcounter{cntRoot}{\x}
            \addtocounter{cntRoot}{1}
            \node[fill=white,draw,circle,inner sep=1pt] at (c)
                {$\sqrt{\thecntRoot}$};
            \coordinate (b) at (c);
            \pgfmathsetcounter{cntShader}{\thecntShader+4}
            \setcounter{cntShader}{\thecntShader}
       }
    }
    \node[fill=white,draw,circle,inner sep=1pt] at (0:1) {$\sqrt{1}$};
\end{tikzpicture}

\end{document}

Comments

#1 Thiago de Melo, December 11, 2008 at 7:37 p.m.

Hello. How can I use \cos(x) and/or \sin(x)? I would like to load a point at (x,\cos(x)), for specifics values of x, like x=\pi/3.

Any idea? Thanks.

#2 Kjell Magne Fauske, December 11, 2008 at 7:55 p.m.

You could try something like this:

    #!latex
    \documentclass{article}
    \usepackage{tikz}

    \begin{document}
    \begin{tikzpicture}
    \foreach \x in {0,0.2,...,{pi/3}}
        \draw (\x,{cos(\x r)}) circle (2pt);
    \end{tikzpicture}
    \end{document}

#3 paul, January 30, 2009 at 11:32 a.m.

It isn't a rooty helix. There is no anything like \x^(0.5). I wrote the similar example of non-rooty helix:

\usetikzlibrary{calc}
\xdefinecolor{darkgreen}{RGB}{175, 193, 36}
\begin{tikzpicture}
    \coordinate (B) at (0,0);
    \foreach \x in {100,99,...,1}{
        \coordinate (C) at (B);
        \coordinate (B) at ({sin(0.2*\x r)*0.2*\x},{cos(0.2*\x r)*0.2*\x});
        \filldraw[fill=darkgreen!\x, draw=gray!\x] (B) -- (C) -- (0,0) -- cycle;
}
\end{tikzpicture}

#4 Felix Lindemann, October 27, 2009 at 6:35 p.m.

@paul ... of course it is a rooty Helix... take a segment of any length (lets assume the length to be \sqrt{x} ) if you attach a lenght of 1 in a right angle in one of the segements ends and you connect the two open ends the segment betweet these ends will have the length of l= \sqrt{(\sqrt{x})^2+1} = \sqrt{x+1} q.e.d.

best regards felix
#5 Håvard Berland, October 12, 2010 at 10:25 p.m.

Felix, your image looks so good, so I copied it to Latex' wikipedia page, at http://en.wikipedia.org/wiki/LaTeX

Adding comments is currently not enabled.

Navigation

Subscribe to the TikZ examples RSS feed

Learn TikZ: TikZ.org

Example: Rooty helix

Comments

Navigation

Features

Tags

Other areas