Shake and Rattle on a planar pendulum example

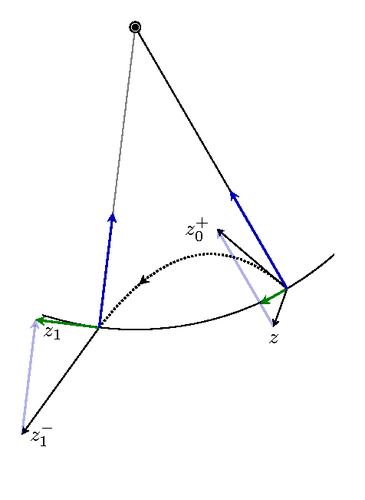
This is an illustration of how the numerical integrator Shake and Rattle work on a simple planar pendulum example. The way it works is by kicking the mass upwards, releasing the constraint, let the mass fly and land back on the constrained set. The drawing is geometrically correct.

Edit and compile if you like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
% Shake and Rattle on a planar pendulum example
% Author: Olivier Verdier
\documentclass{article}
\usepackage{tikz}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{10pt}%
\usetikzlibrary{calc,decorations.markings,intersections,fpu}
 
\tikzset{
  >=stealth,
  fiber/.style  = {draw, thick, blue!70!black},
  flight/.style = {draw, black, thick, densely dotted,
  decoration    = {markings, mark=at position 0.6 with {\arrow{>}}},
  postaction    = {decorate}},
  rattle/.style = {color=green!50!black},
}
 
\begin{document}
\begin{tikzpicture}[
    >=stealth,
    scale                   = 2.5,
    hinge/.style            = {fill=white, draw=black},
    fiber_projection/.style = {opacity=.3, ->},
  ]
  \coordinate (origin) at (0,0);
  \newcommand*\pathfreefall[1]{
    \path[name path=freefall, #1] (2,-3.5) parabola[parabola height=2cm] +(-3,0);
  }
  \newcommand*\pathconstraint[1]{
    \path[name path=constraint, #1] (0,0) circle[radius=2cm];
  }
  % Compute the free fall trajectory by clipping a circle and a parabola
  \begin{scope}
    \pathconstraint{clip}
    \pathfreefall{draw, flight}
  \end{scope}
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX