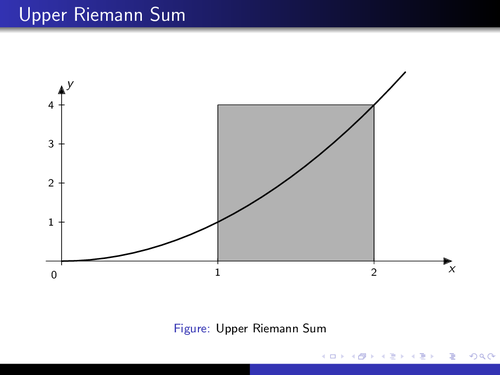
An animation to the area of calculation using the upper Riemann sum.
That's an approximation of an integral by a finite sum, named after the German mathematician Riemann. It is calculated by partitioning the region below the the curve into rectangles and summarizing their areas. To get a better approximation, the region is devided more finely. As the rectangles get smaller, the Rieman sum approaches the Riemann integral. This animation shows it.
Edit and compile if you like:
% Animation for Upper Riemann Sum
% Author: Edson José Teixeira
\documentclass[10pt]{beamer}
\usepackage[controls]{animate}
\usepackage{tikz}
\usetikzlibrary{arrows}
% Beamer Settings
\usetheme{Warsaw}
% Counters
\newcounter{higher}
\setcounter{higher}{1}
\begin{document}
\begin{frame}[fragile]{Upper Riemann Sum}
\begin{figure}
\begin{animateinline}[poster = first, controls]{5}
\whiledo{\thehigher<30}{
\begin{tikzpicture}[line cap=round, line join=round, >=triangle 45,
x=4.0cm, y=1.0cm, scale=1]
\draw [->,color=black] (-0.1,0) -- (2.5,0);
\foreach \x in {1,2}
\draw [shift={(\x,0)}, color=black] (0pt,2pt)
-- (0pt,-2pt) node [below] {\footnotesize $\x$};
\draw [color=black] (2.5,0) node [below] {$x$};
\draw [->,color=black] (0,-0.1) -- (0,4.5);
\foreach \y in {1,2,3,4}
\draw [shift={(0,\y)}, color=black] (2pt,0pt)
-- (-2pt,0pt) node[left] {\footnotesize $\y$};
\draw [color=black] (0,4.5) node [right] {$y$};
\draw [color=black] (0pt,-10pt) node [left] {\footnotesize $0$};
\draw [domain=0:2.2, line width=1.0pt] plot (\x,{(\x)^2});
\clip(0,-0.5) rectangle (3,5);
\draw (2,0) -- (2,4);
\foreach \i in {1,...,\thehigher}
\draw [fill=black,fill opacity=0.3, smooth,samples=50] ({1+(\i-1)/\thehigher},{(1+(\i)/\thehigher)^2})
--({1+(\i)/\thehigher},{(1+(\i)/\thehigher)^2})
-- ({1+(\i)/\thehigher},0)
-- ({1+(\i-1)/\thehigher},0)
-- cycle;
\end{tikzpicture}
%
\stepcounter{higher}
\ifthenelse{\thehigher<30}{ \newframe }{\end{animateinline} }
}
\caption{Upper Riemann Sum}
\end{figure}
\end{frame}
\end{document}Click to download: upper-riemann-sum.tex • upper-riemann-sum.pdf
Open in Overleaf: upper-riemann-sum.tex


