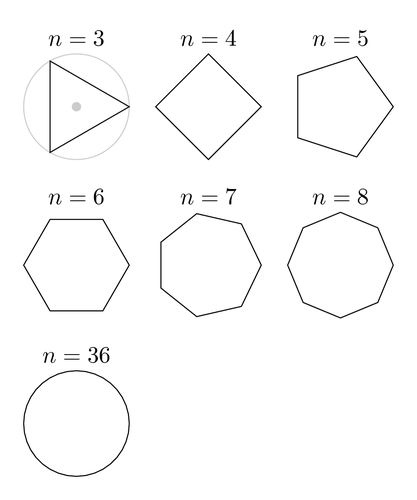
Example of how to draw regular polygons using a \foreach loop inside a path. The angles have been calculated manually.
Update. PGF 1.18
- Fractional angular values are now supported
- Regular polygons are now available as node shapes! See the node shapes example or the manual for more details.
Edit and compile if you like:
% Regular polygons
\documentclass{article}
\usepackage{tikz}
\begin{document}
% Radius of regular polygons
\newdimen\R
\R=0.8cm
\begin{tikzpicture}
% Indicate the boundary of the regular polygons
\draw [thin,black!20] circle (\R) ;
\fill[black!20] circle (2pt);
\draw (0:\R) \foreach \x in {120,240} {
-- (\x:\R)
} -- cycle (90:\R) node[above] {$n=3$} ;
\draw[xshift=2.5\R] (0:\R) \foreach \x in {90,180,...,359} {
-- (\x:\R)
} -- cycle (90:\R) node[above] {$n=4$} ;
\draw[xshift=5.0\R] (0:\R) \foreach \x in {72,144,...,359} {
-- (\x:\R)
} -- cycle (90:\R) node[above] {$n=5$} ;
\begin{scope}[yshift=-3\R]
\draw (0:\R) \foreach \x in {60,120,...,359} {
-- (\x:\R)
}-- cycle (90:\R) node[above] {$n=6$} ;
% 360/7 = 51.4286 For PGF v < 1.18 we have to round to the nearest
% integer. Newer version support fractional angle values.
% For a more accurate result use the sequence
% {51, 103, 154, 206, 257, 309}
%
\draw[xshift=2.5\R] (0:\R) \foreach \x in {51.4286,102.8571,...,359} {
-- (\x:\R)
}-- cycle (90:\R) node[above] {$n=7$} ;
\draw[xshift=5.0\R] (0:\R) \foreach \x in {45,90,...,359} {
-- (\x:\R)
} -- cycle (90:\R) node[above] {$n=8$} ;
\end{scope}
\draw[yshift=-6.0\R] (0:\R) \foreach \x in {10,20,...,359} {
-- (\x:\R)
} -- cycle (90:\R) node[above] {$n=36$} ;
\end{tikzpicture}
\end{document}Click to download: regular-polygons.tex • regular-polygons.pdf
Open in Overleaf: regular-polygons.tex


