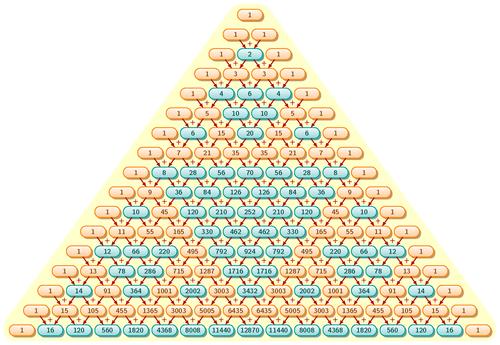
Edit and compile if you like:
%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Author : Paul Gaborit (2009)
% under Creative Commons attribution license.
% Title : Pascal's triangle and Sierpinski triangle
% Note : 17 lines maximum
\documentclass[landscape]{article}
\usepackage[landscape,margin=1cm]{geometry}
\pagestyle{empty}
\usepackage[T1]{fontenc}
\usepackage{lmodern}
\usepackage{tikz}
\usetikzlibrary{positioning,shadows,backgrounds}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{5pt}%
\begin{document}
\centering
\begin{tikzpicture}[x=13mm,y=9mm]
% some colors
\colorlet{even}{cyan!60!black}
\colorlet{odd}{orange!100!black}
\colorlet{links}{red!70!black}
\colorlet{back}{yellow!20!white}
% some styles
\tikzset{
box/.style={
minimum height=5mm,
inner sep=.7mm,
outer sep=0mm,
text width=10mm,
text centered,
font=\small\bfseries\sffamily,
text=#1!50!black,
draw=#1,
line width=.25mm,
top color=#1!5,
bottom color=#1!40,
shading angle=0,
rounded corners=2.3mm,
drop shadow={fill=#1!40!gray,fill opacity=.8},
rotate=0,
},
link/.style={-latex,links,line width=.3mm},
plus/.style={text=links,font=\footnotesize\bfseries\sffamily},
}
% Pascal's triangle
% row #0 => value is 1
\node[box=odd] (p-0-0) at (0,0) {1};
\foreach \row in {1,...,16} {
% col #0 => value is 1
\node[box=odd] (p-\row-0) at (-\row/2,-\row) {1};
\pgfmathsetmacro{\value}{1};
\foreach \col in {1,...,\row} {
% iterative formula : val = precval * (row-col+1)/col
% (+ 0.5 to bypass rounding errors)
\pgfmathtruncatemacro{\value}{\value*((\row-\col+1)/\col)+0.5};
\global\let\value=\value
% position of each value
\coordinate (pos) at (-\row/2+\col,-\row);
% odd color for odd value and even color for even value
\pgfmathtruncatemacro{\rest}{mod(\value,2)}
\ifnum \rest=0
\node[box=even] (p-\row-\col) at (pos) {\value};
\else
\node[box=odd] (p-\row-\col) at (pos) {\value};
\fi
% for arrows and plus sign
\ifnum \col<\row
\node[plus,above=0mm of p-\row-\col]{+};
\pgfmathtruncatemacro{\prow}{\row-1}
\pgfmathtruncatemacro{\pcol}{\col-1}
\draw[link] (p-\prow-\pcol) -- (p-\row-\col);
\draw[link] ( p-\prow-\col) -- (p-\row-\col);
\fi
}
}
\begin{pgfonlayer}{background}
% filling and drawing with the same color to enlarge background
\path[draw=back,fill=back,line width=5mm,rounded corners=2.5mm]
( p-0-0.north west) -- ( p-0-0.north east) --
(p-16-16.north east) -- (p-16-16.south east) --
( p-16-0.south west) -- ( p-16-0.north west) --
cycle;
\end{pgfonlayer}
\end{tikzpicture}
\end{document}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Click to download: pascals-triangle-and-sierpinski-triangle.tex • pascals-triangle-and-sierpinski-triangle.pdf
Open in Overleaf: pascals-triangle-and-sierpinski-triangle.tex