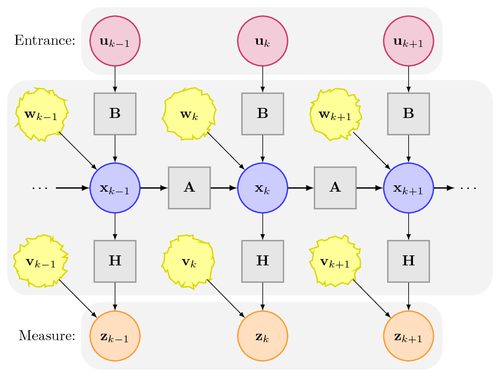
This is the system model of the (linear) Kalman filter.
Edit and compile if you like:
% Kalman filter system model
% by Burkart Lingner
% An example using TikZ/PGF 2.00
%
% Features: Decorations, Fit, Layers, Matrices, Styles
% Tags: Block diagrams, Diagrams
% Technical area: Electrical engineering
\documentclass[a4paper,10pt]{article}
\usepackage[english]{babel}
\usepackage[T1]{fontenc}
\usepackage[ansinew]{inputenc}
\usepackage{lmodern} % font definition
\usepackage{amsmath} % math fonts
\usepackage{amsthm}
\usepackage{amsfonts}
\usepackage{tikz}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{5pt}%
\usetikzlibrary{decorations.pathmorphing} % noisy shapes
\usetikzlibrary{fit} % fitting shapes to coordinates
\usetikzlibrary{backgrounds} % drawing the background after the foreground
\begin{document}
\begin{figure}[htbp]
\centering
% The state vector is represented by a blue circle.
% "minimum size" makes sure all circles have the same size
% independently of their contents.
\tikzstyle{state}=[circle,
thick,
minimum size=1.2cm,
draw=blue!80,
fill=blue!20]
% The measurement vector is represented by an orange circle.
\tikzstyle{measurement}=[circle,
thick,
minimum size=1.2cm,
draw=orange!80,
fill=orange!25]
% The control input vector is represented by a purple circle.
\tikzstyle{input}=[circle,
thick,
minimum size=1.2cm,
draw=purple!80,
fill=purple!20]
% The input, state transition, and measurement matrices
% are represented by gray squares.
% They have a smaller minimal size for aesthetic reasons.
\tikzstyle{matrx}=[rectangle,
thick,
minimum size=1cm,
draw=gray!80,
fill=gray!20]
% The system and measurement noise are represented by yellow
% circles with a "noisy" uneven circumference.
% This requires the TikZ library "decorations.pathmorphing".
\tikzstyle{noise}=[circle,
thick,
minimum size=1.2cm,
draw=yellow!85!black,
fill=yellow!40,
decorate,
decoration={random steps,
segment length=2pt,
amplitude=2pt}]
% Everything is drawn on underlying gray rectangles with
% rounded corners.
\tikzstyle{background}=[rectangle,
fill=gray!10,
inner sep=0.2cm,
rounded corners=5mm]
\begin{tikzpicture}[>=latex,text height=1.5ex,text depth=0.25ex]
% "text height" and "text depth" are required to vertically
% align the labels with and without indices.
% The various elements are conveniently placed using a matrix:
\matrix[row sep=0.5cm,column sep=0.5cm] {
% First line: Control input
&
\node (u_k-1) [input]{$\mathbf{u}_{k-1}$}; &
&
\node (u_k) [input]{$\mathbf{u}_k$}; &
&
\node (u_k+1) [input]{$\mathbf{u}_{k+1}$}; &
\\
% Second line: System noise & input matrix
\node (w_k-1) [noise] {$\mathbf{w}_{k-1}$}; &
\node (B_k-1) [matrx] {$\mathbf{B}$}; &
\node (w_k) [noise] {$\mathbf{w}_k$}; &
\node (B_k) [matrx] {$\mathbf{B}$}; &
\node (w_k+1) [noise] {$\mathbf{w}_{k+1}$}; &
\node (B_k+1) [matrx] {$\mathbf{B}$}; &
\\
% Third line: State & state transition matrix
\node (A_k-2) {$\cdots$}; &
\node (x_k-1) [state] {$\mathbf{x}_{k-1}$}; &
\node (A_k-1) [matrx] {$\mathbf{A}$}; &
\node (x_k) [state] {$\mathbf{x}_k$}; &
\node (A_k) [matrx] {$\mathbf{A}$}; &
\node (x_k+1) [state] {$\mathbf{x}_{k+1}$}; &
\node (A_k+1) {$\cdots$}; \\
% Fourth line: Measurement noise & measurement matrix
\node (v_k-1) [noise] {$\mathbf{v}_{k-1}$}; &
\node (H_k-1) [matrx] {$\mathbf{H}$}; &
\node (v_k) [noise] {$\mathbf{v}_k$}; &
\node (H_k) [matrx] {$\mathbf{H}$}; &
\node (v_k+1) [noise] {$\mathbf{v}_{k+1}$}; &
\node (H_k+1) [matrx] {$\mathbf{H}$}; &
\\
% Fifth line: Measurement
&
\node (z_k-1) [measurement] {$\mathbf{z}_{k-1}$}; &
&
\node (z_k) [measurement] {$\mathbf{z}_k$}; &
&
\node (z_k+1) [measurement] {$\mathbf{z}_{k+1}$}; &
\\
};
% The diagram elements are now connected through arrows:
\path[->]
(A_k-2) edge[thick] (x_k-1) % The main path between the
(x_k-1) edge[thick] (A_k-1) % states via the state
(A_k-1) edge[thick] (x_k) % transition matrices is
(x_k) edge[thick] (A_k) % accentuated.
(A_k) edge[thick] (x_k+1) % x -> A -> x -> A -> ...
(x_k+1) edge[thick] (A_k+1)
(x_k-1) edge (H_k-1) % Output path x -> H -> z
(H_k-1) edge (z_k-1)
(x_k) edge (H_k)
(H_k) edge (z_k)
(x_k+1) edge (H_k+1)
(H_k+1) edge (z_k+1)
(v_k-1) edge (z_k-1) % Output noise v -> z
(v_k) edge (z_k)
(v_k+1) edge (z_k+1)
(w_k-1) edge (x_k-1) % System noise w -> x
(w_k) edge (x_k)
(w_k+1) edge (x_k+1)
(u_k-1) edge (B_k-1) % Input path u -> B -> x
(B_k-1) edge (x_k-1)
(u_k) edge (B_k)
(B_k) edge (x_k)
(u_k+1) edge (B_k+1)
(B_k+1) edge (x_k+1)
;
% Now that the diagram has been drawn, background rectangles
% can be fitted to its elements. This requires the TikZ
% libraries "fit" and "background".
% Control input and measurement are labeled. These labels have
% not been translated to English as "Measurement" instead of
% "Messung" would not look good due to it being too long a word.
\begin{pgfonlayer}{background}
\node [background,
fit=(u_k-1) (u_k+1),
label=left:Entrance:] {};
\node [background,
fit=(w_k-1) (v_k-1) (A_k+1)] {};
\node [background,
fit=(z_k-1) (z_k+1),
label=left:Measure:] {};
\end{pgfonlayer}
\end{tikzpicture}
\caption{Kalman filter system model}
\end{figure}
This is the system model of the (linear) Kalman filter. At each time
step the state vector $\mathbf{x}_k$ is propagated to the new state
estimation $\mathbf{x}_{k+1}$ by multiplication with the constant state
transition matrix $\mathbf{A}$. The state vector $\mathbf{x}_{k+1}$ is
additionally influenced by the control input vector $\mathbf{u}_{k+1}$
multiplied by the input matrix $\mathbf{B}$, and the system noise vector
$\mathbf{w}_{k+1}$. The system state cannot be measured directly. The
measurement vector $\mathbf{z}_k$ consists of the information contained
within the state vector $\mathbf{x}_k$ multiplied by the measurement
matrix $\mathbf{H}$, and the additional measurement noise $\mathbf{v}_k$.
\end{document}
Click to download: kalman-filter.tex • kalman-filter.pdf
Open in Overleaf: kalman-filter.tex


