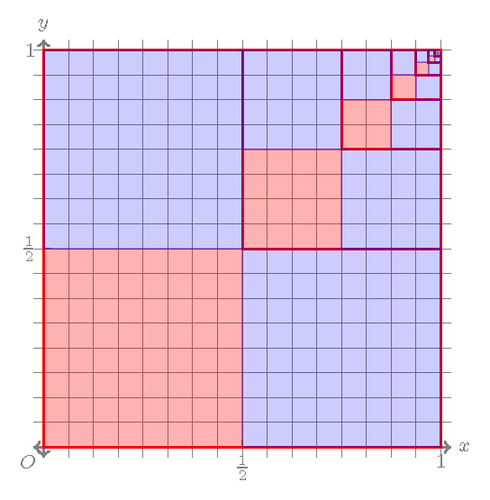
The infinite series 1/4 + 1/16 + 1/64 + 1/256 + ... is one of the first computed infinite series in the history of mathematics, already used by Archimedes. Its sum is 1/3.
Edit and compile if you like:
% Geometric representation of the sum 1/4 + 1/16 + 1/64 + 1/256 + ...
% Author: Jimi Oke
\documentclass{article}
\usepackage{tikz}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{5pt}%
\begin{document}
\begin{tikzpicture}[scale=.35]\footnotesize
\pgfmathsetmacro{\xone}{-.4}
\pgfmathsetmacro{\xtwo}{ 16.4}
\pgfmathsetmacro{\yone}{-.4}
\pgfmathsetmacro{\ytwo}{16.4}
\begin{scope}<+->;
% grid
\draw[step=1cm,gray,very thin] (\xone,\yone) grid (\xtwo,\ytwo);
% ticks
\foreach \x/\xtext in { 8/\frac{1}{2}, 16/1}
\draw[gray,xshift=\x cm] (0,.3) -- (0,0) node[below] {$\xtext$};
\foreach \y/\ytext in {8/\frac{1}{2},16/1}
\draw[gray, yshift=\y cm] (.3,0) -- (0,0)
node[left] {$\ytext$};
% origin
\draw[gray] (0,0) node[anchor=north east] {$O$};
% axes
\draw[gray,thick,<->] (\xone, 0) -- (\xtwo, 0) node[right] {$x$};
\draw[gray,thick,<->] (0, \yone) -- (0, \ytwo) node[above] {$y$};
\end{scope}
% function
\begin{scope}[thick,red]
\foreach \x in {16, 8, 4, 2, 1,.5,.25}
\draw (16-\x, 16-\x) rectangle (16,16);
\foreach \x in {16, 8, 4, 2, 1,.5,.25}
\filldraw[thin,red,opacity=.3] (16-\x, 16-\x)
rectangle (16-.5*\x,16-.5*\x);
\foreach \x in {16, 8, 4, 2, 1,.5,.25}{
\filldraw[thin,blue,opacity=.2] (16-\x, 16-.5*\x)
rectangle (16-.5*\x,16);
\filldraw[thin,blue,opacity=.2] (16-.5*\x, 16-\x)
rectangle (16,16-.5*\x);}
\end{scope}
\end{tikzpicture}
\end{document}
Click to download: geometric-series.tex • geometric-series.pdf
Open in Overleaf: geometric-series.tex


