Edit and compile if you like:
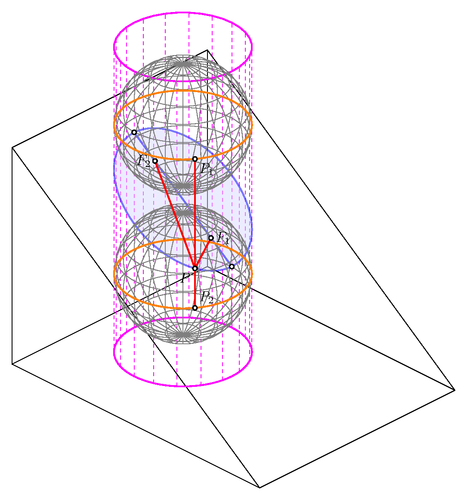
% Plane Sections of the Cylinder - Dandelin Spheres
% Author: Hugues Vermeiren
\documentclass{article}
\usepackage{tikz}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{10pt}%
\tikzset{
MyPersp/.style={scale=1.8,x={(-0.8cm,-0.4cm)},y={(0.8cm,-0.4cm)},
z={(0cm,1cm)}},
% MyPersp/.style={scale=1.5,x={(0cm,0cm)},y={(1cm,0cm)},
% z={(0cm,1cm)}}, % uncomment the two lines to get a lateral view
MyPoints/.style={fill=white,draw=black,thick}
}
\begin{document}
\begin{tikzpicture}[MyPersp,font=\large]
% the base circle is the unit circle in plane Oxy
\def\h{2.5}% Heigth of the ellipse center (on the axis of the cylinder)
\def\a{35}% angle of the section plane with the horizontal
\def\aa{35}% angle that defines position of generatrix PA--PB
\pgfmathparse{\h/tan(\a)}
\let\b\pgfmathresult
\pgfmathparse{sqrt(1/cos(\a)/cos(\a)-1)}
\let\c\pgfmathresult %Center Focus distance of the section ellipse.
\pgfmathparse{\c/sin(\a)}
\let\p\pgfmathresult % Position of Dandelin spheres centers
% on the Oz axis (\h +/- \p)
\coordinate (A) at (2,\b,0);
\coordinate (B) at (-2,\b,0);
\coordinate (C) at (-2,-1.5,{(1.5+\b)*tan(\a)});
\coordinate (D) at (2,-1.5,{(1.5+\b)*tan(\a)});
\coordinate (E) at (2,-1.5,0);
\coordinate (F) at (-2,-1.5,0);
\coordinate (CLS) at (0,0,{\h-\p});
\coordinate (CUS) at (0,0,{\h+\p});
\coordinate (FA) at (0,{\c*cos(\a)},{-\c*sin(\a)+\h});% Focii
\coordinate (FB) at (0,{-\c*cos(\a)},{\c*sin(\a)+\h});
\coordinate (SA) at (0,1,{-tan(\a)+\h}); % Vertices of the
% great axes of the ellipse
\coordinate (SB) at (0,-1,{tan(\a)+\h});
\coordinate (PA) at ({sin(\aa},{cos(\aa)},{\h+\p});
\coordinate (PB) at ({sin(\aa},{cos(\aa)},{\h-\p});
\coordinate (P) at ({sin(\aa)},{cos(\aa)},{-tan(\a)*cos(\aa)+\h});
% Point on the ellipse on generatrix PA--PB
\draw (A)--(B)--(C)--(D)--cycle;
\draw (D)--(E)--(F)--(C);
\draw (A)--(E) (B)--(F);
\draw[blue,very thick] (SA)--(SB);
% \coordinate (O) at (0,0,0);
% \draw[->] (O)--(2.5,0,0)node[below left]{x};
% \draw[->] (O)--(0,3,0)node[right]{y};
% \draw[->] (O)--(0,0,6)node[left]{z};
\foreach \t in {20,40,...,360}% generatrices
\draw[magenta,dashed] ({cos(\t)},{sin(\t)},0)
--({cos(\t)},{sin(\t)},{2.0*\h});
\draw[magenta,very thick] (1,0,0) % lower circle
\foreach \t in {5,10,...,360}
{--({cos(\t)},{sin(\t)},0)}--cycle;
\draw[magenta,very thick] (1,0,{2*\h}) % upper circle
\foreach \t in {10,20,...,360}
{--({cos(\t)},{sin(\t)},{2*\h})}--cycle;
\fill[blue!15,draw=blue,very thick,opacity=0.5]
(0,1,{\h-tan(\a)}) % elliptical section
\foreach \t in {5,10,...,360}
{--({sin(\t)},{cos(\t)},{-tan(\a)*cos(\t)+\h})}--cycle;
\foreach \i in {-1,1}{%Spheres!
\foreach \t in {0,15,...,165}% meridians
{\draw[gray] ({cos(\t)},{sin(\t)},\h+\i*\p)
\foreach \rho in {5,10,...,360}
{--({cos(\t)*cos(\rho)},{sin(\t)*cos(\rho)},
{sin(\rho)+\h+\i*\p})}--cycle;
}
\foreach \t in {-75,-60,...,75}% parallels
{\draw[gray] ({cos(\t)},0,{sin(\t)+\h+\i*\p})
\foreach \rho in {5,10,...,360}
{--({cos(\t)*cos(\rho)},{cos(\t)*sin(\rho)},
{sin(\t)+\h+\i*\p})}--cycle;
}
\draw[orange,very thick] (1,0,{\h+\i*\p})% Equators
\foreach \t in {5,10,...,360}
{--({cos(\t)},{sin(\t)},{\h+\i*\p})}--cycle;
}
\draw[red,very thick] (PA)--(PB);
\draw[red,very thick] (FA)--(P)--(FB);
% \fill[MyPoints] (CLS) circle (1pt);% center of lower sphere
% \fill[MyPoints] (CUS) circle (1pt);% center of upper sphere
\fill[MyPoints] (FA) circle (1pt)node[right]{$F_1$};
\fill[MyPoints] (FB) circle (1pt)node[left]{$F_2$};
\fill[MyPoints] (SA) circle (1pt);
\fill[MyPoints] (SB) circle (1pt);
\fill[MyPoints] (P) circle (1pt)node[below left]{$P$};
\fill[MyPoints] (PA) circle (1pt)node[below right]{$P_1$};
\fill[MyPoints] (PB) circle (1pt)node[above right]{$P_2$};
\end{tikzpicture}
\end{document}
Click to download: dandelin-spheres.tex • dandelin-spheres.pdf
Open in Overleaf: dandelin-spheres.tex


