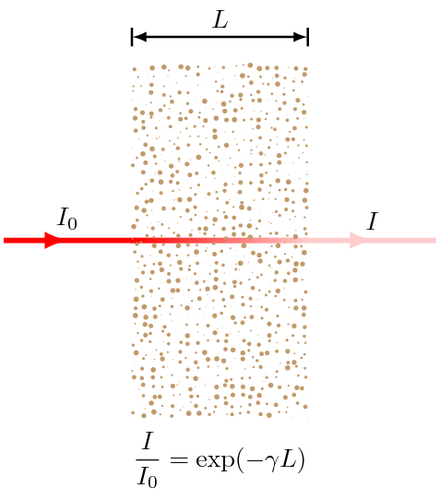
The Lambert-Beer law states there is a logarithmic dependence between the ratio between incident light intensity $I_0$ and the intensity of scattered light directing forward $I$ through a media and the product of the absorption coefficient $gamma$ of the substance and the distance the light travels through the material $L$.
I/I_0 = exp(-gamma L)
In the case of the figure above, the light is a red laser beam through a cloud formed by sand grains with a certain granulometry schematized with spherical particles.To deep the argument ($gamma$ computation), see "Light scattering by small particles" by Hulst van de H.C., Dover Publications.
Edit and compile if you like:
% Lambert-Beer law parameters drawing
% Author: Michele Muccioli
% Compile with LuaLaTeX
\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{calc,fadings,decorations.markings}
\usepackage{amsmath}
%%%%%%%%%%%%%%%%%%%%%%%%%%%
% FADING LIGHT DECORATION %
%%%%%%%%%%%%%%%%%%%%%%%%%%%
\makeatletter
\pgfkeys{/pgf/decoration/.cd,
start color/.store in = \startcolor,
end color/.store in = \endcolor
}
\pgfdeclaredecoration{color change}{initial}{
% Initial state
\state{initial}[%
width = 0pt,
next state = line,
persistent precomputation = {\pgfmathdivide{50}{\pgfdecoratedpathlength}%
\let\increment=\pgfmathresult%
\def\x{0}}]%
{}%
% Line state
\state{line}[%
width = .5pt,
persistent postcomputation = {\pgfmathadd@{\x}{\increment}%
\let\x=\pgfmathresult}]%
{%
\pgfsetlinewidth{\pgflinewidth}%
\pgfsetarrows{-}%
\pgfpathmoveto{\pgfpointorigin}%
\pgfpathlineto{\pgfqpoint{.75pt}{0pt}}%
\pgfsetstrokecolor{\endcolor!\x!\startcolor}%
\pgfusepath{stroke}%
}%
% Final state
\state{final}{%
\pgfsetlinewidth{\pgflinewidth}%
\pgfpathmoveto{\pgfpointorigin}%
\color{\endcolor!\x!\startcolor}%
\pgfusepath{stroke}%
}
}
\makeatother
%%%%%%%%%%%%
% COMMANDS %
%%%%%%%%%%%%
\def\pr#1{\directlua{tex.print(#1)}}
\def\rnd{.%
\pdfuniformdeviate10%
\pdfuniformdeviate10%
\pdfuniformdeviate10%
}
\begin{document}
%%%%%%%%%%%%%%
% PARAMETERS %
%%%%%%%%%%%%%%
\definecolor{sand}{RGB}{193,154,107} % Particles color
\def\cols{20} % Number of columns
\def\rows{40} % Number of rows
\def\SquareUnit{.35} % Lengths of unit square edges (cm)
\pgfmathsetmacro\RmaxParticle{.1} % Maximum particle radius
\def\BeforeLight{5} % Light path before particle cloud
\begin{tikzpicture}[x = \SquareUnit cm,
y = \SquareUnit cm,
line width = 2pt
]
%%%%%%%%%%%%%%
% LIGHT PATH %
%%%%%%%%%%%%%%
%-> Before particles cloud
\draw[red,
decoration = {markings,
mark = at position 0.5 with {\arrow[]{latex}}},
postaction = {decorate}] (-\BeforeLight,{\rows*\SquareUnit/2})--++
(\BeforeLight,0)node[midway,
above,
black]{$I_0$};
%-> Trespassing particles cloud
\draw[decoration = {color change,
start color = red,
end color = red!20!white},
decorate] (0,{\rows*\SquareUnit/2})--++
(\cols*\SquareUnit,0);
%-> After particles cloud
\draw[red!20!white,
decoration = {markings,
mark = at position 0.5 with {\arrow[]{latex}}},
postaction = {decorate}] ({\cols*\SquareUnit},{\rows*\SquareUnit/2})--++
(\BeforeLight,0)node[midway,
above,
black]{$I$};
%%%%%%%%%%%%%%%%%%%
% PARTICLES CLOUD %
%%%%%%%%%%%%%%%%%%%
%-> Lua version (FASTER)
\foreach \i in {1,...,\cols}{
\foreach \j in {1,...,\rows}{
\edef\radius{\pr{\RmaxParticle*math.random()}}
\edef\l{\pr{\SquareUnit-2*\radius}}
\edef\x{\pr{(\i-1)*\SquareUnit+\radius+\l*math.random()}}
\edef\y{\pr{(\j-1)*\SquareUnit+\radius+\l*math.random()}}
\fill[sand] (\x,\y)circle[radius=\radius];
}
}
%-> pgfmath version (uncomment it if you want to try)
% Some time compilation gives too high
% number computation problem
%\foreach \i in {1,...,\cols}{
% \foreach \j in {1,...,\rows}{
% \pgfmathsetmacro\radius{\RmaxParticle*\rnd}
% \pgfmathsetmacro\l{\SquareUnit-2*\radius}
% \pgfmathsetmacro\x{(\i-1)*\SquareUnit+\radius+\l*\rnd}
% \pgfmathsetmacro\y{(\j-1)*\SquareUnit+\radius+\l*\rnd}
% \fill[sand] (\x,\y)circle[radius=\radius];
% }
%}
%%%%%%%%%%%%%%%%%%
% LENGTH QUOTING %
%%%%%%%%%%%%%%%%%%
\draw[|<->|,
> = latex,
line width = .8pt] ($(0,\rows*\SquareUnit)+(0,1)$)--++
(\cols*\SquareUnit,0)node[midway,
above]{$L$};
%%%%%%%%%%%%%%%%%%%%
% LAMBERT-BEER LAW %
%%%%%%%%%%%%%%%%%%%%
\node[anchor = north,
inner sep = 1ex] at (current bounding box.south){$\dfrac{I}{I_0}=\exp(-\gamma L)$};
\end{tikzpicture}
\end{document}
Click to download: lambert-beer-law.tex • lambert-beer-law.pdf
Open in Overleaf: lambert-beer-law.tex


