Animation for Upper Riemann Sum

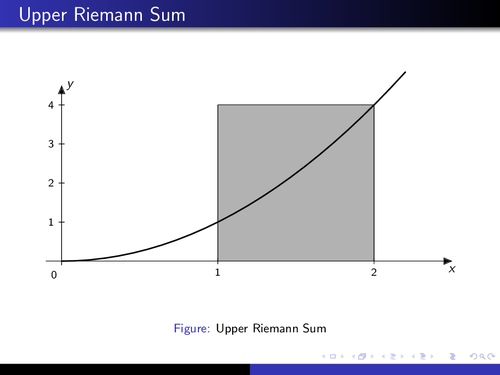
An animation to the area of calculation using the upper Riemann sum.

That's an approximation of an integral by a finite sum, named after the German mathematician Riemann. It is calculated by partitioning the region below the the curve into rectangles and summarizing their areas. To get a better approximation, the region is devided more finely. As the rectangles get smaller, the Rieman sum approaches the Riemann integral. This animation shows it.

Edit and compile if you like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
% Animation for Upper Riemann Sum
% Author: Edson José Teixeira
\documentclass[10pt]{beamer}
\usepackage[controls]{animate}
\usepackage{tikz}
\usetikzlibrary{arrows}
% Beamer Settings
\usetheme{Warsaw}
% Counters
\newcounter{higher} 
\setcounter{higher}{1}
\begin{document}
\begin{frame}[fragile]{Upper Riemann Sum}
  \begin{figure}
    \begin{animateinline}[poster = first, controls]{5}
      \whiledo{\thehigher<30}{
        \begin{tikzpicture}[line cap=round, line join=round, >=triangle 45,
                            x=4.0cm, y=1.0cm, scale=1]
          \draw [->,color=black] (-0.1,0) -- (2.5,0);
          \foreach \x in {1,2}
            \draw [shift={(\x,0)}, color=black] (0pt,2pt)
                  -- (0pt,-2pt) node [below] {\footnotesize $\x$};
          \draw [color=black] (2.5,0) node [below] {$x$};
          \draw [->,color=black] (0,-0.1) -- (0,4.5);
          \foreach \y in {1,2,3,4}
            \draw [shift={(0,\y)}, color=black] (2pt,0pt)
                  -- (-2pt,0pt) node[left] {\footnotesize $\y$};
          \draw [color=black] (0,4.5) node [right] {$y$};
          \draw [color=black] (0pt,-10pt) node [left] {\footnotesize $0$};
          \draw [domain=0:2.2, line width=1.0pt] plot (\x,{(\x)^2});
          \clip(0,-0.5) rectangle (3,5);
          \draw (2,0) -- (2,4);
          \foreach \i in {1,...,\thehigher}
            \draw [fill=black,fill opacity=0.3, smooth,samples=50] ({1+(\i-1)/\thehigher},{(1+(\i)/\thehigher)^2})
                  --({1+(\i)/\thehigher},{(1+(\i)/\thehigher)^2})
                  --  ({1+(\i)/\thehigher},0)
                  -- ({1+(\i-1)/\thehigher},0)
                  -- cycle;
        \end{tikzpicture}
        %
        \stepcounter{higher}
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX