One of the nicest things about programming illustrations, is that it's easy to change parameters. In this example I've parameterized a three link manipulator using a macro. I can then draw the manipulator in different positions with just one line of code.
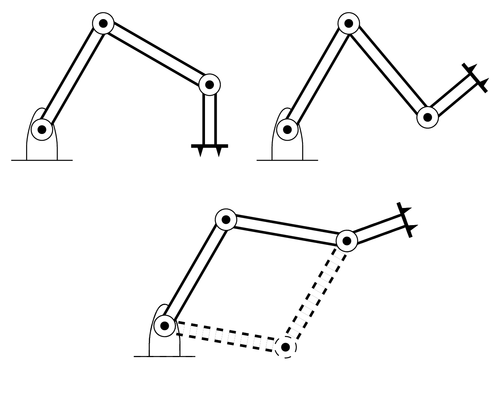
Edit and compile if you like:
\documentclass{article}
\usepackage[latin1]{inputenc}
\usepackage{tikz}
\usetikzlibrary{patterns}
\begin{document}
\pagestyle{empty}
% Note. This illustration was originally made with PSTricks. Conversion to
% PGF/TikZ was straightforward. However, I could probably have made it more
% elegant.
% Define a variable as a length
\newcommand{\nvar}[2]{%
\newlength{#1}
\setlength{#1}{#2}
}
% Define a few constants for drawing
\nvar{\dg}{0.3cm}
\def\dw{0.25}\def\dh{0.5}
% Define commands for links, joints and such
\def\link{\draw [double distance=1.5mm, very thick] (0,0)--}
\def\joint{%
\filldraw [fill=white] (0,0) circle (5pt);
\fill[black] circle (2pt);
}
\def\grip{%
\draw[ultra thick](0cm,\dg)--(0cm,-\dg);
\fill (0cm, 0.5\dg)+(0cm,1.5pt) -- +(0.6\dg,0cm) -- +(0pt,-1.5pt);
\fill (0cm, -0.5\dg)+(0cm,1.5pt) -- +(0.6\dg,0cm) -- +(0pt,-1.5pt);
}
\def\robotbase{%
\draw[rounded corners=8pt] (-\dw,-\dh)-- (-\dw, 0) --
(0,\dh)--(\dw,0)--(\dw,-\dh);
\draw (-0.5,-\dh)-- (0.5,-\dh);
\fill[pattern=north east lines] (-0.5,-1) rectangle (0.5,-\dh);
}
% This macro draws a three link manipulator.
% Input parameters:
% #1 theta_1
% #2 L_1
% #3 theta_2
% #4 L_2
% #5 theta_3
% #6 L_3
%
% Example:
% \threelink{60}{2}{-70}{2}{30}{1}
\newcommand{\threelink}[6]{%
\robotbase
\link(#1:#2);
\joint
\begin{scope}[shift=(#1:#2), rotate=#1]
\link(#3:#4);
\joint
\begin{scope}[shift=(#3:#4), rotate=#3]
\link(#5:#6);
\joint
\begin{scope}[shift=(#5:#6), rotate=#5]
\grip
\end{scope}
\end{scope}
\end{scope}
}
\begin{tikzpicture}
\threelink{60}{2}{-90}{2}{-60}{1}
\begin{scope}[xshift=4cm]
\threelink{60}{2}{-110}{2}{90}{1}
\end{scope}
\begin{scope}[shift={(2cm, -3.2cm)}]
% Illustration of two different solutions to the inverse kinematic
% problem.
\begin{scope}[dashed]
\threelink{-10}{2}{70}{2}{-40}{1}
\end{scope}
\threelink{60}{2}{-70}{2}{30}{1}
\end{scope}
\end{tikzpicture}
\end{document}Click to download: three-link-manipulator.tex • three-link-manipulator.pdf
Open in Overleaf: three-link-manipulator.tex


