Radix-2 signal flow graph for a 16 point fast Fourier transform (FFT). This diagram is quite complex. However, the most difficult part is keeping track of all the indexes. The foreach command is used extensively to get compact code.
Source: The diagram was inspired by content on this web page.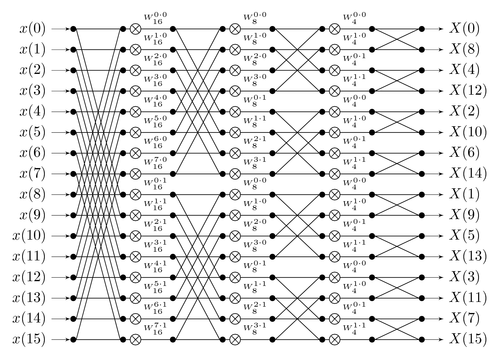
Edit and compile if you like:
\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{arrows}
\begin{document}
\pagestyle{empty}
\tikzstyle{n}= [circle, fill, minimum size=4pt,inner sep=0pt, outer sep=0pt]
\tikzstyle{mul} = [circle,draw,inner sep=-1pt]
% Define two helper counters
\newcounter{x}\newcounter{y}
\begin{tikzpicture}[yscale=0.5, xscale=1.2, node distance=0.3cm, auto]
% The strategy is to create nodes with names: N-column-row
% Input nodes are named N-0-0 ... N-0-15
% Output nodes are named N-10-0 ... N-10-15
% Draw inputs
\foreach \y in {0,...,15}
\node[n, pin={[pin edge={latex'-,black}]left:$x(\y)$}]
(N-0-\y) at (0,-\y) {};
% Draw outputs
\foreach \y / \idx in {0/0,1/8,2/4,3/12,4/2,5/10,6,7/14,
8/1,9,10/5,11/13,12/3,13/11,14/7,15}
\node[n, pin={[pin edge={-latex',black}]right:$X(\idx)$}]
(N-10-\y) at (7,-\y) {};
% draw connector nodes
\foreach \y in {0,...,15}
\foreach \x / \c in {1/1,2/3,3/4,4/6,5/7,6/9}
\node[n, name=N-\c-\y] at (\x,-\y) {};
% draw x nodes
\foreach \y in {0,...,15}
\foreach \x / \c in {1/2,4/5,7/8}
\node[mul, right of=N-\x-\y] (N-\c-\y) {${\times}$};
% horizontal connections
% Note the use of simple counter arithmetics to get correct
% indexes.
\foreach \y in {0,...,15}
\foreach \x in {0,1,3,4,6,7,9}
{
\setcounter{x}{\x}\stepcounter{x}
\path (N-\x-\y) edge[-] (N-\arabic{x}-\y);
}
% Draw the W_16 coefficients
\setcounter{y}{0}
\foreach \i / \j in {0/0,1/0,2/0,3/0,4/0,5/0,6/0,7/0,
0/1,1/1,2/1,3/1,4/1,5/1,6/1,7/1}
{
\path (N-2-\arabic{y}) edge[-] node {\tiny $W^{\i\cdot\j}_{16}$}
(N-3-\arabic{y});
\stepcounter{y}
}
% Draw the W_8 coefficients
\setcounter{y}{0}
\foreach \i / \j in {0/0,1/0,2/0,3/0,0/1,1/1,2/1,3/1,
0/0,1/0,2/0,3/0,0/1,1/1,2/1,3/1}
{
\path (N-5-\arabic{y}) edge[-] node {\tiny $W^{\i\cdot\j}_{8}$}
(N-6-\arabic{y});
\addtocounter{y}{1}
}
% Draw the W_4 coefficients
\setcounter{y}{0}
\foreach \i / \j in {0/0,1/0,0/1,1/1,0/0,1/0,0/1,1/1,
0/0,1/0,0/1,1/1,0/0,1/0,0/1,1/1}
{
\path (N-8-\arabic{y}) edge[-] node {\tiny $W^{\i\cdot\j}_{4}$}
(N-9-\arabic{y});
\stepcounter{y}
}
% Connect nodes
\foreach \sourcey / \desty in {0/8,1/9,2/10,3/11,
4/12,5/13,6/14,7/15,
8/0,9/1,10/2,11/3,
12/4,13/5,14/6,15/7}
\path (N-0-\sourcey.east) edge[-] (N-1-\desty.west);
\foreach \sourcey / \desty in {0/4,1/5,2/6,3/7,
4/0,5/1,6/2,7/3,
8/12,9/13,10/14,11/15,
12/8,13/9,14/10,15/11}
\path (N-3-\sourcey.east) edge[-] (N-4-\desty.west);
\foreach \sourcey / \desty in {0/2,1/3,2/0,3/1,
4/6,5/7,6/4,7/5,
8/10,9/11,10/8,11/9,
12/14,13/15,14/12,15/13}
\path (N-6-\sourcey.east) edge[-] (N-7-\desty.west);
\foreach \sourcey / \desty in {0/1,1/0,2/3,3/2,
4/5,5/4,6/7,7/6,
8/9,9/8,10/11,11/10,
12/13,13/12,14/15,15/14}
\path (N-9-\sourcey.east) edge[-] (N-10-\desty.west);
\end{tikzpicture}
\end{document}
Click to download: radix2fft.tex • radix2fft.pdf
Open in Overleaf: radix2fft.tex


