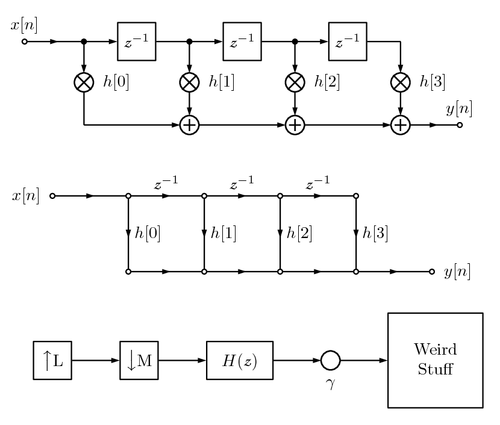
This library is an extension of the example of Karlheinz Ochs [1] and provides basic building blocks for block diagrams and signal flow graphs. The provided example illustrates a finite impulse response (FIR) filter as block diagram and signal flow graph.
[1] /signal-flow-building-blocks/
Edit and compile if you like:
% Library for block diagrams and signal flow graphs
% Author: Matthias Hotz
\documentclass{article}
\usepackage{tikz}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength{\PreviewBorder}{10pt}%
\usetikzlibrary{dsp,chains}
\DeclareMathAlphabet{\mathpzc}{OT1}{pzc}{m}{it}
\newcommand{\z}{\mathpzc{z}}
\begin{document}
% FIR filter as block diagram
\begin{tikzpicture}
% Place nodes using a matrix
\matrix (m1) [row sep=2.5mm, column sep=5mm]
{
%--------------------------------------------------------------------
\node[dspnodeopen,dsp/label=above] (m00) {$x[n]$}; &
\node[coordinate] (m01) {}; &
\node[dspnodefull] (m02) {}; &
\node[dspsquare] (m03) {$\z^{-1}$}; &
\node[dspnodefull] (m04) {}; &
\node[dspsquare] (m05) {$\z^{-1}$}; &
\node[dspnodefull] (m06) {}; &
\node[dspsquare] (m07) {$\z^{-1}$}; &
\node[coordinate] (m08) {}; &
\node[coordinate] (m09) {}; &
\node[coordinate] (m0X) {}; \\
%--------------------------------------------------------------------
\node[coordinate] (m10) {}; &
\node[coordinate] (m11) {}; &
\node[dspmixer, dsp/label=right] (m12) {$h[0]$}; &
\node[coordinate] (m13) {}; &
\node[dspmixer, dsp/label=right] (m14) {$h[1]$}; &
\node[coordinate] (m15) {}; &
\node[dspmixer, dsp/label=right] (m16) {$h[2]$}; &
\node[coordinate] (m17) {}; &
\node[dspmixer, dsp/label=right] (m18) {$h[3]$}; &
\node[coordinate] (m19) {}; &
\node[coordinate] (m1X) {}; \\
%--------------------------------------------------------------------
\\
%--------------------------------------------------------------------
\node[coordinate] (m20) {}; &
\node[coordinate] (m21) {}; &
\node[coordinate] (m22) {}; &
\node[coordinate] (m23) {}; &
\node[dspadder] (m24) {}; &
\node[coordinate] (m25) {}; &
\node[dspadder] (m26) {}; &
\node[coordinate] (m27) {}; &
\node[dspadder] (m28) {}; &
\node[coordinate] (m29) {}; &
\node[dspnodeopen,dsp/label=above] (m2X) {$y[n]$}; \\
%--------------------------------------------------------------------
};
% Draw connections
\begin{scope}[start chain]
\chainin (m00);
\chainin (m02) [join=by dspflow];
\chainin (m12) [join=by dspconn];
\chainin (m22) [join=by dspline];
\end{scope}
\foreach \i [evaluate = \i as \j using int(\i+1),
evaluate = \i as \k using int(\i+2),] in {2,4,6}
{
\begin{scope}[start chain]
\chainin (m0\i);
\chainin (m0\j) [join=by dspconn];
\chainin (m0\k) [join=by dspline];
\chainin (m1\k) [join=by dspconn];
\chainin (m2\k) [join=by dspconn];
\end{scope}
\draw[dspconn] (m2\i) -- (m2\k);
}
\draw[dspflow] (m28) -- (m2X);
% Place nodes using another matrix for another picture
\matrix (m2) [row sep=15mm, column sep=15mm, below=of m1]
{
%--------------------------------------------------------------------
\node[dspnodeopen,dsp/label=left] (m00) {$x[n]$}; &
\node[dspnodeopen] (m01) {}; &
\node[dspnodeopen] (m02) {}; &
\node[dspnodeopen] (m03) {}; &
\node[dspnodeopen] (m04) {}; &
\node[coordinate] (m05) {}; \\
%--------------------------------------------------------------------
\node[coordinate] (m10) {}; &
\node[dspnodeopen] (m11) {}; &
\node[dspnodeopen] (m12) {}; &
\node[dspnodeopen] (m13) {}; &
\node[dspnodeopen] (m14) {}; &
\node[dspnodeopen,dsp/label=right] (m15) {$y[n]$}; \\
%--------------------------------------------------------------------
};
% Draw connections
\draw[dspflow] (m00) -- (m01);
\foreach \i [evaluate = \i as \j using int(\i+1)] in {1,2,3}
\draw[dspflow] (m0\i) -- node[midway,above] {$\z^{-1}$} (m0\j);
\foreach \i [evaluate = \i as \j using int(\i-1)] in {1,2,...,4}
\draw[dspflow] (m0\i) -- node[midway,right] {$h[\j]$} (m1\i);
\foreach \i [evaluate = \i as \j using int(\i+1)] in {1,2,...,4}
\draw[dspflow] (m1\i) -- (m1\j);
% Other elements
\node[dspsquare, below=of m10, below=10ex] (c0) {\upsamplertext{L}};
\node[dspsquare,right= of c0] (c1) {\downsamplertext{M}};
\node[dspfilter,right=of c1] (c2) {$H(\z)$};
\node[dspmultiplier,right=of c2,dsp/label=below] (c3) {$\gamma$};
\node[dspfilter,right=of c3,minimum size=2cm,text height=2em]
(c4) {Weird\\ Stuff};
\foreach \i [evaluate = \i as \j using int(\i+1)] in {0,1,...,3}
\draw[dspconn] (c\i) -- (c\j);
\end{tikzpicture}
\end{document}
Click to download: fir-filter.tex • fir-filter.pdf
Open in Overleaf: fir-filter.tex


