Energy level diagrams – illustrating Hund’s rule

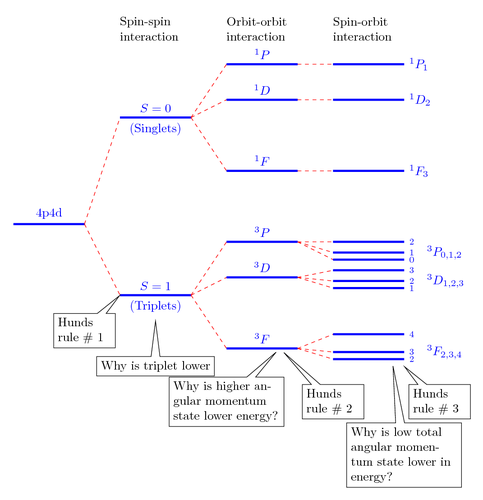
Here we illustrate Hund's rules, which is a set of rules in atomic physics written by the German physicist Friedrich Hund. They are used to determine the term symbol corresponding to the ground state of a multi-electron atom.

All the coloring is done using styles so it is easy to change the style of the drawing.

The code was written by Henri Menke and published on TeX.SE.

Edit and compile if you like:

% Energy level diagrams - illustrating Hund's rule
% Author: Henri Menke
\documentclass[tikz, border=10pt]{standalone}
\usetikzlibrary{shapes.callouts}
\tikzset{
  level/.style   = { ultra thick, blue },
  connect/.style = { dashed, red },
  notice/.style  = { draw, rectangle callout, callout relative pointer={#1} },
  label/.style   = { text width=2cm }
}
\begin{document}
\begin{tikzpicture}
   % Draw all levels
  \draw[level] (0,0) -- node[above] {4p4d} (2,0);

  \draw[connect] (2,0)  -- (3,-2) (2,0) -- (3,3);
  \draw[level]   (3,3)  -- node[above] {$S=0$} node[below] {(Singlets)} (5,3);
  \draw[level]   (3,-2) -- node[above] {$S=1$} node[below] {(Triplets)} (5,-2);

  \draw[connect] (5,3)    -- (6,4.5) (5,3) -- (6,3.5) (5,3) -- (6,1.5);
  \draw[connect] (5,-2)   -- (6,-0.5) (5,-2) -- (6,-1.5) (5,-2) -- (6,-3.5);
  \draw[level]   (6,4.5)  -- node[above] {${}^1P$} (8,4.5);
  \draw[level]   (6,3.5)  -- node[above] {${}^1D$} (8,3.5);
  \draw[level]   (6,1.5)  -- node[above] {${}^1F$} (8,1.5);
  \draw[level]   (6,-0.5) -- node[above] {${}^3P$} (8,-0.5);
  \draw[level]   (6,-1.5) -- node[above] {${}^3D$} (8,-1.5);
  \draw[level]   (6,-3.5) -- node[above] {${}^3F$} (8,-3.5);

  \draw[connect] (8,4.5) -- (9,4.5) (8,3.5) -- (9,3.5) (8,1.5) -- (9,1.5);
  \draw[level]   (9,4.5) -- (11,4.5) node[right] {${}^1P_1$};
  \draw[level]   (9,3.5) -- (11,3.5) node[right] {${}^1D_2$};
  \draw[level]   (9,1.5) -- (11,1.5) node[right] {${}^1F_3$};

  \draw[connect] (8,-0.5) -- (9,-0.5) (8,-0.5) -- (9,-0.8) (8,-0.5) -- (9,-1)
                 (8,-1.5) -- (9,-1.6) (8,-1.5) -- (9,-1.8) (8,-1.5) -- (9,-1.3)
                 (8,-3.5) -- (9,-3.8) (8,-3.5) -- (9,-3.6) (8,-3.5) -- (9,-3.1);
  \foreach \i/\j in {2/-0.5, 1/-0.8, 0/-1} {
    \draw[level] (9,\j) -- (11,\j) node[right] {\scriptsize $\i$};
  }
  \node[level, right] at (11.5,-0.8) {${}^3P_{0,1,2}$};
  \foreach \i/\j in {3/-1.3, 2/-1.6, 1/-1.8} {
    \draw[level] (9,\j) -- (11,\j) node[right] {\scriptsize $\i$};
  }
  \node[level, right] at (11.5,-1.6) {${}^3D_{1,2,3}$};
  \foreach \i/\j in {4/-3.1, 3/-3.6, 2/-3.8} {
    \draw[level] (9,\j) -- (11,\j) node[right] {\scriptsize $\i$};
  }
  \node[level, right] at (11.5,-3.6) {${}^3F_{2,3,4}$};

  % Draw labels
  \node[label] at (4,5.5)  {Spin-spin interaction};
  \node[label] at (7,5.5)  {Orbit-orbit interaction};
  \node[label] at (10,5.5) {Spin-orbit interaction};

  % Draw annotations
  \node[notice={(0.5,0.5)}, text width=1.5cm] at (2,-3) {Hunds rule \# 1};
  \node[notice={(0,1)}] at (4,-4) {Why is triplet lower};
  \node[notice={(0.7,0.7)}, text width=3cm] at (6,-5)
    {Why is higher angular momentum state lower energy?};
  \node[notice={(-0.9,0.9)}, text width=1.5cm] at (9,-5) {Hunds rule \# 2};
  \node[notice={(-0.2,1.6)}, text width=3cm] at (11,-6.5)
    {Why is low total angular momentum state lower in energy?};
  \node[notice={(-0.5,0.5)}, text width=1.5cm] at (12,-5) {Hunds rule \# 3};
\end{tikzpicture}
\end{document}